Matrix Free Total Derivatives#
The compute_jacvec_product method of Problem can be used to compute a matrix free total Jacobian vector product. It’s analogous to the way that the compute_jacvec_product method of System can be used to compute partial Jacobian vector products.
- Problem.compute_jacvec_product(of, wrt, mode, seed)[source]
Given a seed and ‘of’ and ‘wrt’ variables, compute the total jacobian vector product.
- Parameters:
- oflist of str
Variables whose derivatives will be computed.
- wrtlist of str
Derivatives will be computed with respect to these variables.
- modestr
Derivative direction (‘fwd’ or ‘rev’).
- seeddict or list
Either a dict keyed by ‘wrt’ varnames (fwd) or ‘of’ varnames (rev), containing dresidual (fwd) or doutput (rev) values, OR a list of dresidual or doutput values that matches the corresponding ‘wrt’ (fwd) or ‘of’ (rev) varname list.
- Returns:
- dict
The total jacobian vector product, keyed by variable name.
Below is an example of a component that embeds a sub-problem and uses compute_jacvec_product on that sub-problem to compute its Jacobian. The SubProbComp component computes derivatives in both ‘fwd’ and ‘rev’ directions, but in a realistic scenario, it would only compute them in a single direction.
The model that SubProbComp is intended to emulate is one that looks like this:
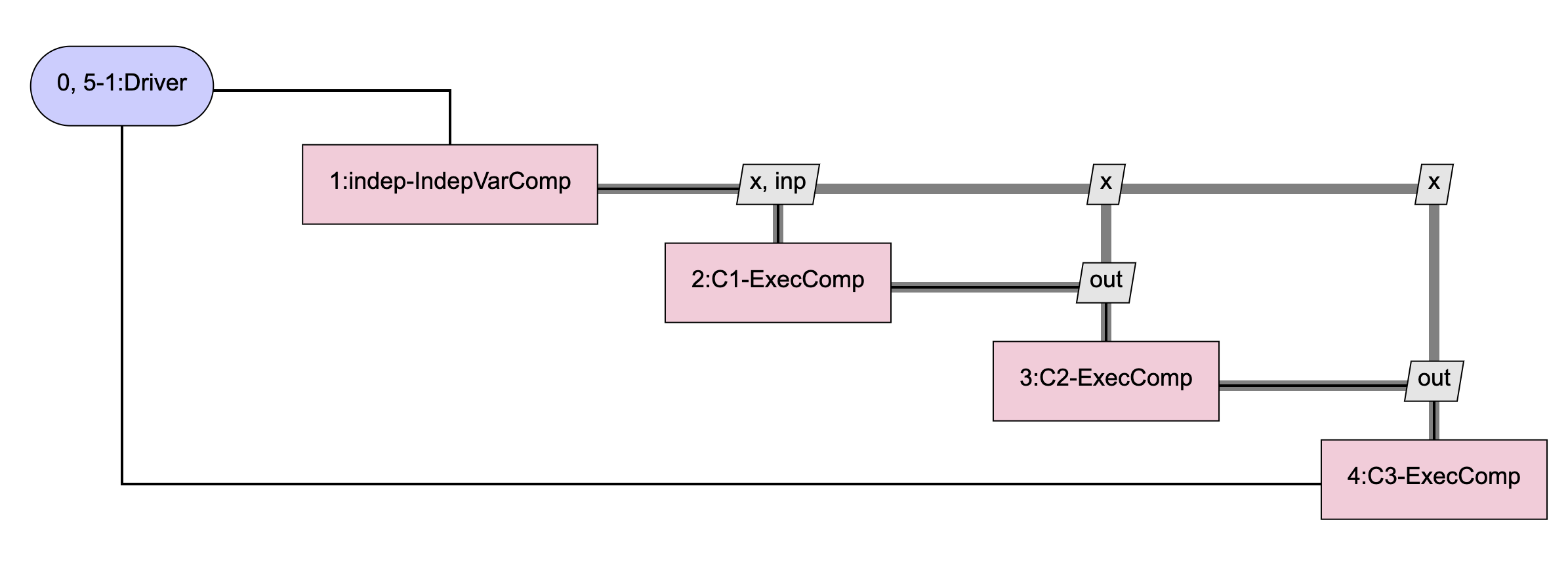
Instead of using 3 identical ExecComps as shown above and having OpenMDAO automatically compute the total derivatives for us, SubProbComp will use just a single ExecComp and will compute its derivatives internally. The model contained in the sub-problem looks like this:
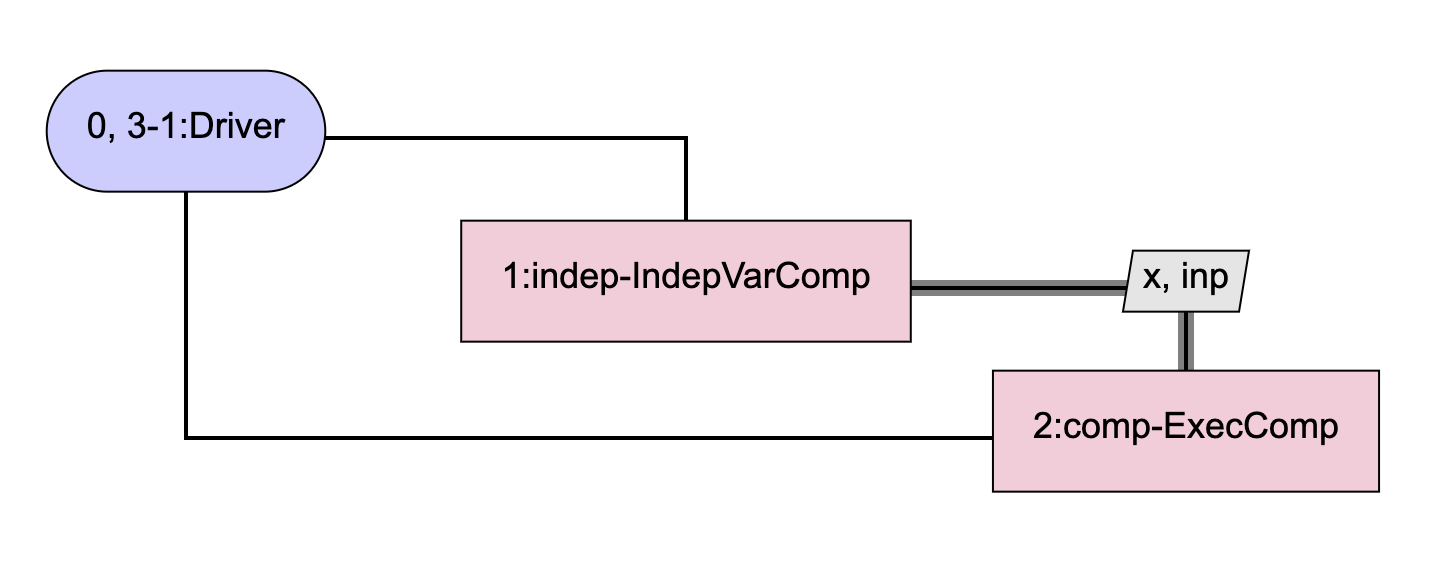
The code for SubProbComp is shown below:
import openmdao.api as om
class SubProbComp(om.ExplicitComponent):
"""
This component contains a sub-Problem with a component that will be solved over num_nodes
points instead of creating num_nodes instances of that same component and connecting them
together.
"""
def __init__(self, input_size, num_nodes, mode, **kwargs):
super().__init__(**kwargs)
self.prob = None
self.size = input_size
self.num_nodes = num_nodes
self.mode = mode
def _setup_subprob(self):
self.prob = p = om.Problem(comm=self.comm)
model = self.prob.model
model.add_subsystem('comp', get_comp(self.size))
p.setup()
p.final_setup()
def setup(self):
self._setup_subprob()
self.add_input('x', np.zeros(self.size - 1))
self.add_input('inp', val=0.0)
self.add_output('out', val=0.0)
self.declare_partials('*', '*')
def compute(self, inputs, outputs):
p = self.prob
p['comp.x'] = inputs['x']
p['comp.inp'] = inputs['inp']
inp = inputs['inp']
for i in range(self.num_nodes):
p['comp.inp'] = inp
p.run_model()
inp = p['comp.out']
outputs['out'] = p['comp.out']
def _compute_partials_fwd(self, inputs, partials):
p = self.prob
x = inputs['x']
p['comp.x'] = x
p['comp.inp'] = inputs['inp']
seed = {'comp.x':np.zeros(x.size), 'comp.inp': np.zeros(1)}
p.run_model()
p.model._linearize()
for rhsname in seed:
for rhs_i in range(seed[rhsname].size):
seed['comp.x'][:] = 0.0
seed['comp.inp'][:] = 0.0
seed[rhsname][rhs_i] = 1.0
for i in range(self.num_nodes):
p.model._vectors['output']['linear'].set_val(0.0)
p.model._vectors['residual']['linear'].set_val(0.0)
jvp = p.compute_jacvec_product(of=['comp.out'], wrt=['comp.x','comp.inp'], mode='fwd', seed=seed)
seed['comp.inp'][:] = jvp['comp.out']
if rhsname == 'comp.x':
partials[self.pathname + '.out', self.pathname +'.x'][0, rhs_i] = jvp[self.pathname + '.out']
else:
partials[self.pathname + '.out', self.pathname + '.inp'][0, 0] = jvp[self.pathname + '.out']
def _compute_partials_rev(self, inputs, partials):
p = self.prob
p['comp.x'] = inputs['x']
p['comp.inp'] = inputs['inp']
seed = {'comp.out': np.ones(1)}
stack = []
comp = p.model.comp
comp._inputs['inp'] = inputs['inp']
# store the inputs to each comp (the comp at each node point) by doing nonlinear solves
# and storing what the inputs are for each node point. We'll set these inputs back
# later when we linearize about each node point.
for i in range(self.num_nodes):
stack.append(comp._inputs['inp'][0])
comp._inputs['x'] = inputs['x']
comp._solve_nonlinear()
comp._inputs['inp'] = comp._outputs['out']
for i in range(self.num_nodes):
p.model._vectors['output']['linear'].set_val(0.0)
p.model._vectors['residual']['linear'].set_val(0.0)
comp._inputs['inp'] = stack.pop()
comp._inputs['x'] = inputs['x']
p.model._linearize()
jvp = p.compute_jacvec_product(of=['comp.out'], wrt=['comp.x','comp.inp'], mode='rev', seed=seed)
seed['comp.out'][:] = jvp['comp.inp']
# all of the comp.x's are connected to the same indepvarcomp, so we have
# to accumulate their contributions together
partials[self.pathname + '.out', self.pathname + '.x'] += jvp['comp.x']
# this one doesn't get accumulated because each comp.inp contributes to the
# previous comp's .out (or to comp.inp in the case of the first comp) only.
# Note that we have to handle this explicitly here because normally in OpenMDAO
# we accumulate derivatives when we do reverse transfers. We can't do that
# here because we only have one instance of our component, so instead of
# accumulating into separate 'comp.out' variables for each comp instance,
# we would be accumulating into a single comp.out variable, which would make
# our derivative too big.
partials[self.pathname + '.out', self.pathname + '.inp'] = jvp['comp.inp']
def compute_partials(self, inputs, partials):
# note that typically you would only have to define partials for one direction,
# either fwd OR rev, not both.
if self.mode == 'fwd':
self._compute_partials_fwd(inputs, partials)
else:
self._compute_partials_rev(inputs, partials)
