Converging an Implicit Model: Nonlinear circuit analysis

Consider a simple electrical circuit made up from two resistors, a diode, and a constant current source. Our goal is to solve for the steady-state voltages at node 1 and node 2.

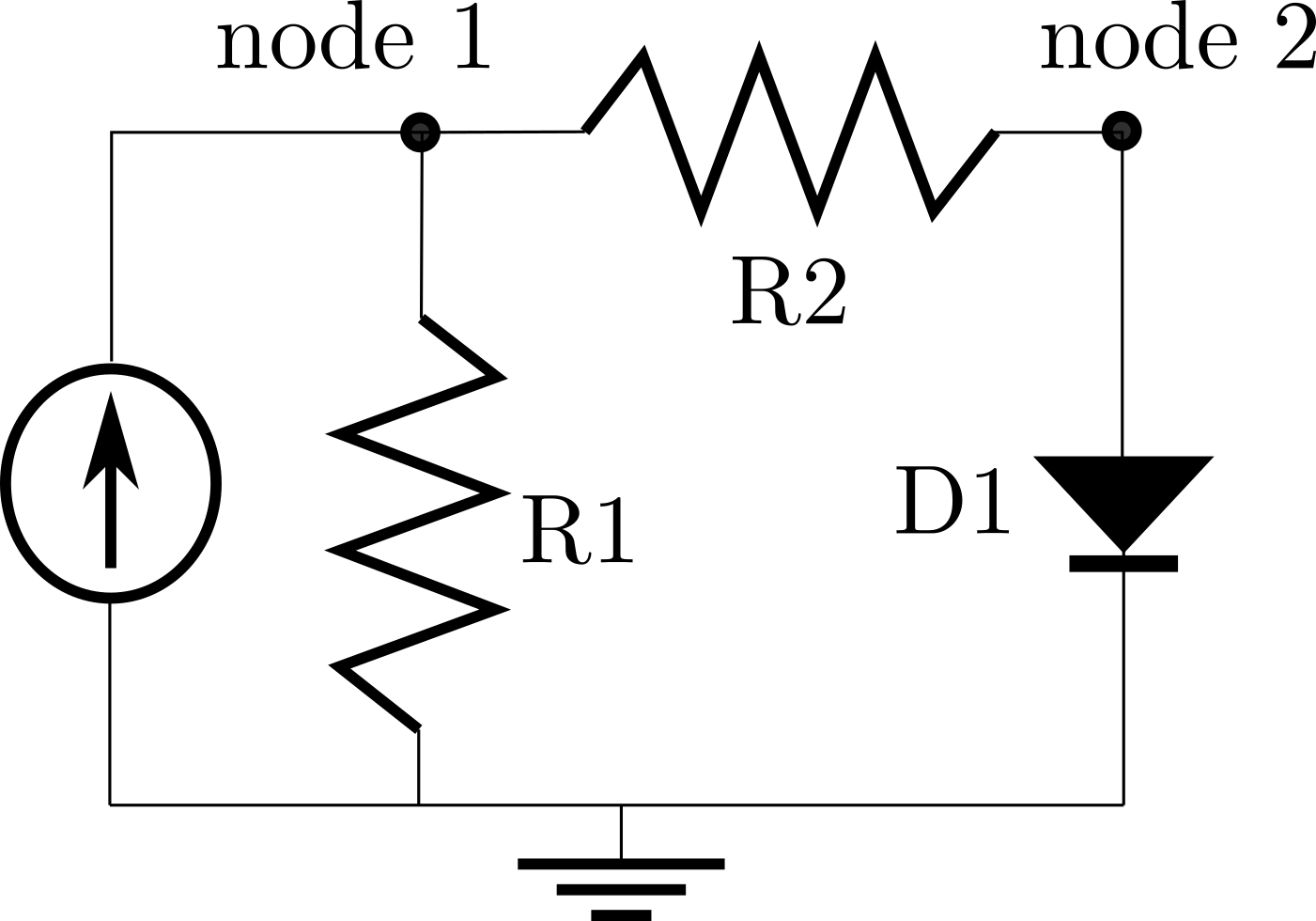
In order to find the voltages, we’ll employ Kirchoff’s current law, and solve for the voltages needed at each node to drive the net-current to 0.

import numpy as np

import openmdao.api as om


class Resistor(om.ExplicitComponent):
    """Computes current across a resistor using Ohm's law."""

    def initialize(self):
        self.options.declare('R', default=1., desc='Resistance in Ohms')

    def setup(self):
        self.add_input('V_in', units='V')
        self.add_input('V_out', units='V')
        self.add_output('I', units='A')

        # partial derivs are constant, so we can assign their values in setup
        R = self.options['R']
        self.declare_partials('I', 'V_in', val=1 / R)
        self.declare_partials('I', 'V_out', val=-1 / R)

    def compute(self, inputs, outputs):
        deltaV = inputs['V_in'] - inputs['V_out']
        outputs['I'] = deltaV / self.options['R']

class Diode(om.ExplicitComponent):
    """Computes current across a diode using the Shockley diode equation."""

    def initialize(self):
        self.options.declare('Is', default=1e-15, desc='Saturation current in Amps')
        self.options.declare('Vt', default=.025875, desc='Thermal voltage in Volts')

    def setup(self):
        self.add_input('V_in', units='V')
        self.add_input('V_out', units='V')
        self.add_output('I', units='A')

        # non-linear component, so we'll declare the partials here but compute them in compute_partials
        self.declare_partials('I', 'V_in')
        self.declare_partials('I', 'V_out')

    def compute(self, inputs, outputs):
        deltaV = inputs['V_in'] - inputs['V_out']
        Is = self.options['Is']
        Vt = self.options['Vt']
        outputs['I'] = Is * (np.exp(deltaV / Vt) - 1)

    def compute_partials(self, inputs, J):
        deltaV = inputs['V_in'] - inputs['V_out']
        Is = self.options['Is']
        Vt = self.options['Vt']
        I = Is * np.exp(deltaV / Vt)

        J['I', 'V_in'] = I/Vt
        J['I', 'V_out'] = -I/Vt

class Node(om.ImplicitComponent):
    """Computes voltage residual across a node based on incoming and outgoing current."""

    def initialize(self):
        self.options.declare('n_in', default=1, types=int, desc='number of connections with + assumed in')
        self.options.declare('n_out', default=1, types=int, desc='number of current connections + assumed out')

    def setup(self):
        self.add_output('V', val=5., units='V')

        for i in range(self.options['n_in']):
            i_name = 'I_in:{}'.format(i)
            self.add_input(i_name, units='A')
            self.declare_partials('V', i_name, val=1)

        for i in range(self.options['n_out']):
            i_name = 'I_out:{}'.format(i)
            self.add_input(i_name, units='A')
            self.declare_partials('V', i_name, val=-1)

            # note: we don't declare any partials wrt `V` here,
            #      because the residual doesn't directly depend on it

    def apply_nonlinear(self, inputs, outputs, residuals):
        residuals['V'] = 0.
        for i_conn in range(self.options['n_in']):
            residuals['V'] += inputs['I_in:{}'.format(i_conn)]
        for i_conn in range(self.options['n_out']):
            residuals['V'] -= inputs['I_out:{}'.format(i_conn)]

class Circuit(om.Group):

    def setup(self):
        self.add_subsystem('n1', Node(n_in=1, n_out=2), promotes_inputs=[('I_in:0', 'I_in')])
        self.add_subsystem('n2', Node())  # leaving defaults

        self.add_subsystem('R1', Resistor(R=100.), promotes_inputs=[('V_out', 'Vg')])
        self.add_subsystem('R2', Resistor(R=10000.))
        self.add_subsystem('D1', Diode(), promotes_inputs=[('V_out', 'Vg')])

        self.connect('n1.V', ['R1.V_in', 'R2.V_in'])
        self.connect('R1.I', 'n1.I_out:0')
        self.connect('R2.I', 'n1.I_out:1')

        self.connect('n2.V', ['R2.V_out', 'D1.V_in'])
        self.connect('R2.I', 'n2.I_in:0')
        self.connect('D1.I', 'n2.I_out:0')

        self.nonlinear_solver = om.NewtonSolver()
        self.linear_solver = om.DirectSolver()

        self.nonlinear_solver.options['iprint'] = 2
        self.nonlinear_solver.options['maxiter'] = 10
        self.nonlinear_solver.options['solve_subsystems'] = True
        self.nonlinear_solver.linesearch = om.ArmijoGoldsteinLS()
        self.nonlinear_solver.linesearch.options['maxiter'] = 10
        self.nonlinear_solver.linesearch.options['iprint'] = 2


p = om.Problem()
model = p.model

model.add_subsystem('circuit', Circuit())

p.setup()

p.set_val('circuit.I_in', 0.1)
p.set_val('circuit.Vg', 0.)

# set some initial guesses
p.set_val('circuit.n1.V', 10.)
p.set_val('circuit.n2.V', 1e-3)

p.run_model()

print(p['circuit.n1.V'])
print(p['circuit.n2.V'])
print(p['circuit.R1.I'])
print(p['circuit.R2.I'])
print(p['circuit.D1.I'])

# sanity check: should sum to .1 Amps
print(p['circuit.R1.I'] + p['circuit.D1.I'])

=======
circuit
=======
NL: Newton 0 ; 0.00141407214 1
|  LS: AG 1 ; 6.9707252e+152 1
|  LS: AG 2 ; 8.51199079e+68 0.5
|  LS: AG 3 ; 9.40605982e+26 0.25
|  LS: AG 4 ; 988771.709 0.125
|  LS: AG 5 ; 0.00130322117 0.0625
NL: Newton 1 ; 0.00130322117 0.921608691
|  LS: AG 1 ; 5580826.07 1
|  LS: AG 2 ; 13.3748871 0.5
|  LS: AG 3 ; 0.0198015756 0.25
|  LS: AG 4 ; 0.000828003297 0.125
NL: Newton 2 ; 0.000828003297 0.585545301
NL: Newton 3 ; 7.02986117e-06 0.00497135964
NL: Newton 4 ; 2.64550002e-08 1.87083809e-05
NL: Newton 5 ; 3.78431444e-13 2.67618202e-10
NL: Newton Converged
[9.90804735]
[0.71278185]
[0.09908047]
[0.00091953]
[0.00091953]
[0.1]