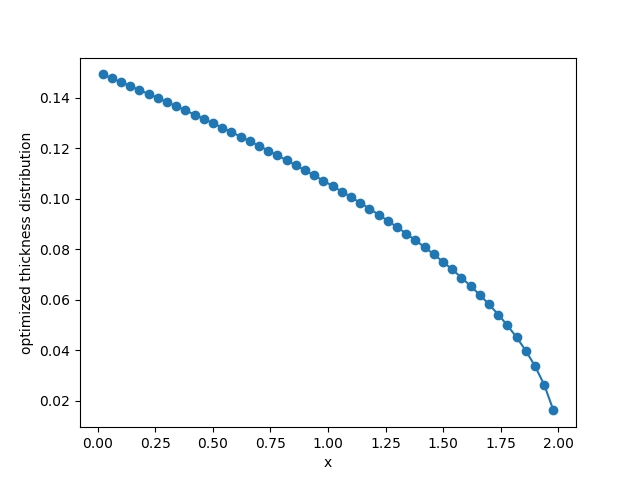
Optimizing the Thickness Distribution of a Cantilever Beam Using the Adjoint Method#
In this example, we optimize the thickness (height) distribution of a cantilever beam using the adjoint method to compute the gradient. We use Euler–Bernoulli beam theory and assume a rectangular section.
Background#
The optimization problem is:
\[\begin{split}
\begin{array}{r c l}
\text{minimize} & & f^T d \\
\text{with respect to} & & h \\
\text{subject to} & & \text{sum}(h) b L_0 = \text{volume} \\
\end{array}
\end{split}\]
where \(f\) is the vector of forces, \(h\) is the vector of beam heights, and \(L_0\) is the length of a single beam element.
The displacements vector \(d\) is given by
\[
K d = f
\]
where \(K\) is the stiffness matrix. However, in practice, we augment the linear system with Lagrange multipliers to apply the boundary constraints at the first node.
Since our model contains a system of equations, we use the adjoint method to compute the gradient of the objective with respect to the beam height vector. The model is shown below.
/usr/share/miniconda/envs/test/lib/python3.11/site-packages/scipy/optimize/_slsqp_py.py:437: RuntimeWarning: Values in x were outside bounds during a minimize step, clipping to bounds
fx = wrapped_fun(x)
Optimization terminated successfully (Exit mode 0)
Current function value: 23762.153677443166
Iterations: 153
Function evaluations: 462
Gradient evaluations: 153
Optimization Complete
-----------------------------------
Implementation: list of components#
There are 5 components that compute:
Moment of inertia for each element
Local stiffness matrix for each element
Displacements from solution of the \(Kd=f\) linear system augmented with the Lagrange multipliers
Compliance
Volume
class MomentOfInertiaComp(om.ExplicitComponent):
def initialize(self):
self.options.declare('num_elements', types=int)
self.options.declare('b')
def setup(self):
num_elements = self.options['num_elements']
self.add_input('h', shape=num_elements)
self.add_output('I', shape=num_elements)
def setup_partials(self):
rows = cols = np.arange(self.options['num_elements'])
self.declare_partials('I', 'h', rows=rows, cols=cols)
def compute(self, inputs, outputs):
outputs['I'] = 1./12. * self.options['b'] * inputs['h'] ** 3
def compute_partials(self, inputs, partials):
partials['I', 'h'] = 1./4. * self.options['b'] * inputs['h'] ** 2
class LocalStiffnessMatrixComp(om.ExplicitComponent):
def initialize(self):
self.options.declare('num_elements', types=int)
self.options.declare('E')
self.options.declare('L')
def setup(self):
num_elements = self.options['num_elements']
E = self.options['E']
L = self.options['L']
self.add_input('I', shape=num_elements)
self.add_output('K_local', shape=(num_elements, 4, 4))
L0 = L / num_elements
coeffs = np.empty((4, 4))
coeffs[0, :] = [12, 6 * L0, -12, 6 * L0]
coeffs[1, :] = [6 * L0, 4 * L0 ** 2, -6 * L0, 2 * L0 ** 2]
coeffs[2, :] = [-12, -6 * L0, 12, -6 * L0]
coeffs[3, :] = [6 * L0, 2 * L0 ** 2, -6 * L0, 4 * L0 ** 2]
coeffs *= E / L0 ** 3
self.mtx = np.zeros((num_elements, 4, 4, num_elements))
for ind in range(num_elements):
self.mtx[ind, :, :, ind] = coeffs
self.declare_partials('K_local', 'I',
val=self.mtx.reshape(16 * num_elements, num_elements))
def compute(self, inputs, outputs):
outputs['K_local'] = 0
for ind in range(self.options['num_elements']):
outputs['K_local'][ind, :, :] = self.mtx[ind, :, :, ind] * inputs['I'][ind]
from scipy.sparse import coo_matrix
from scipy.sparse.linalg import splu
class StatesComp(om.ImplicitComponent):
def initialize(self):
self.options.declare('num_elements', types=int)
self.options.declare('force_vector', types=np.ndarray)
def setup(self):
num_elements = self.options['num_elements']
num_nodes = num_elements + 1
size = 2 * num_nodes + 2
self.add_input('K_local', shape=(num_elements, 4, 4))
self.add_output('d', shape=size)
cols = np.arange(16*num_elements)
rows = np.repeat(np.arange(4), 4)
rows = np.tile(rows, num_elements) + np.repeat(np.arange(num_elements), 16) * 2
self.declare_partials('d', 'K_local', rows=rows, cols=cols)
self.declare_partials('d', 'd')
def apply_nonlinear(self, inputs, outputs, residuals):
force_vector = np.concatenate([self.options['force_vector'], np.zeros(2)])
self.K = self.assemble_CSC_K(inputs)
residuals['d'] = self.K.dot(outputs['d']) - force_vector
def solve_nonlinear(self, inputs, outputs):
force_vector = np.concatenate([self.options['force_vector'], np.zeros(2)])
self.K = self.assemble_CSC_K(inputs)
self.lu = splu(self.K)
outputs['d'] = self.lu.solve(force_vector)
def linearize(self, inputs, outputs, jacobian):
num_elements = self.options['num_elements']
self.K = self.assemble_CSC_K(inputs)
self.lu = splu(self.K)
i_elem = np.tile(np.arange(4), 4)
i_d = np.tile(i_elem, num_elements) + np.repeat(np.arange(num_elements), 16) * 2
jacobian['d', 'K_local'] = outputs['d'][i_d]
jacobian['d', 'd'] = self.K.toarray()
def solve_linear(self, d_outputs, d_residuals, mode):
if mode == 'fwd':
d_outputs['d'] = self.lu.solve(d_residuals['d'])
else:
d_residuals['d'] = self.lu.solve(d_outputs['d'])
def assemble_CSC_K(self, inputs):
"""
Assemble the stiffness matrix in sparse CSC format.
Returns
-------
ndarray
Stiffness matrix as dense ndarray.
"""
num_elements = self.options['num_elements']
num_nodes = num_elements + 1
num_entry = num_elements * 12 + 4
ndim = num_entry + 4
data = np.zeros((ndim, ), dtype=inputs._get_data().dtype)
cols = np.empty((ndim, ))
rows = np.empty((ndim, ))
# First element.
data[:16] = inputs['K_local'][0, :, :].flat
cols[:16] = np.tile(np.arange(4), 4)
rows[:16] = np.repeat(np.arange(4), 4)
j = 16
for ind in range(1, num_elements):
ind1 = 2 * ind
K = inputs['K_local'][ind, :, :]
# NW quadrant gets summed with previous connected element.
data[j-6:j-4] += K[0, :2]
data[j-2:j] += K[1, :2]
# NE quadrant
data[j:j+4] = K[:2, 2:].flat
rows[j:j+4] = np.array([ind1, ind1, ind1 + 1, ind1 + 1])
cols[j:j+4] = np.array([ind1 + 2, ind1 + 3, ind1 + 2, ind1 + 3])
# SE and SW quadrants together
data[j+4:j+12] = K[2:, :].flat
rows[j+4:j+12] = np.repeat(np.arange(ind1 + 2, ind1 + 4), 4)
cols[j+4:j+12] = np.tile(np.arange(ind1, ind1 + 4), 2)
j += 12
data[-4:] = 1.0
rows[-4] = 2 * num_nodes
rows[-3] = 2 * num_nodes + 1
rows[-2] = 0.0
rows[-1] = 1.0
cols[-4] = 0.0
cols[-3] = 1.0
cols[-2] = 2 * num_nodes
cols[-1] = 2 * num_nodes + 1
n_K = 2 * num_nodes + 2
return coo_matrix((data, (rows, cols)), shape=(n_K, n_K)).tocsc()
class ComplianceComp(om.ExplicitComponent):
def initialize(self):
self.options.declare('num_elements', types=int)
self.options.declare('force_vector', types=np.ndarray)
def setup(self):
num_nodes = self.options['num_elements'] + 1
self.add_input('displacements', shape=2 * num_nodes)
self.add_output('compliance')
def setup_partials(self):
num_nodes = self.options['num_elements'] + 1
force_vector = self.options['force_vector']
self.declare_partials('compliance', 'displacements',
val=force_vector.reshape((1, 2 * num_nodes)))
def compute(self, inputs, outputs):
outputs['compliance'] = np.dot(self.options['force_vector'], inputs['displacements'])
class VolumeComp(om.ExplicitComponent):
def initialize(self):
self.options.declare('num_elements', types=int)
self.options.declare('b', default=1.)
self.options.declare('L')
def setup(self):
num_elements = self.options['num_elements']
b = self.options['b']
L = self.options['L']
L0 = L / num_elements
self.add_input('h', shape=num_elements)
self.add_output('volume')
self.declare_partials('volume', 'h', val=b * L0)
def compute(self, inputs, outputs):
L0 = self.options['L'] / self.options['num_elements']
outputs['volume'] = np.sum(inputs['h'] * self.options['b'] * L0)
Implementation: Optimization Script#
Here is the optimization script:
from openmdao.test_suite.test_examples.beam_optimization.beam_group import BeamGroup
E = 1.
L = 1.
b = 0.1
volume = 0.01
num_elements = 50
prob = om.Problem(model=BeamGroup(E=E, L=L, b=b, volume=volume, num_elements=num_elements))
prob.driver = om.ScipyOptimizeDriver()
prob.driver.options['optimizer'] = 'SLSQP'
prob.driver.options['tol'] = 1e-9
prob.driver.options['disp'] = True
prob.setup()
prob.run_driver()
print(prob['h'])
Optimization terminated successfully (Exit mode 0)
Current function value: 23762.153677443166
Iterations: 153
Function evaluations: 462
Gradient evaluations: 153
Optimization Complete
-----------------------------------
[0.14915761 0.14764324 0.1461133 0.14456712 0.14300417 0.14142411
0.13982611 0.13820961 0.136574 0.13491861 0.1332426 0.1315454
0.12982571 0.12808319 0.12631652 0.12452489 0.12270697 0.12086182
0.11898815 0.11708425 0.11514905 0.11318068 0.1111776 0.10913769
0.10705878 0.10493902 0.10277541 0.10056526 0.09830545 0.09599249
0.0936224 0.09119084 0.0886926 0.086122 0.08347231 0.08073578
0.07790321 0.07496385 0.07190452 0.0687093 0.06535833 0.06182633
0.05808048 0.0540766 0.04975295 0.04501849 0.03972912 0.03363155
0.02620192 0.01610863]
