Wind Turbine Actuator Disc

Optimizing an Actuator Disc Model to Find Betz Limit for Wind Turbines

The Betz limit is the theoretical maximum amount of kinetic energy that a wind turbine can extract from the flow. This limit was derived analytically by Albert Betz in 1919, but it can also be found numerically using an optimizer and a simple actuator disc model for a wind-turbine.

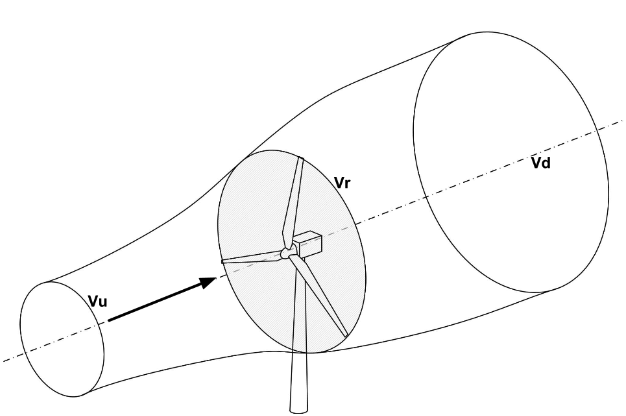
The Actuator Disc Model

import openmdao.api as om


class ActuatorDisc(om.ExplicitComponent):
    """Simple wind turbine model based on actuator disc theory"""

    def setup(self):

        # Inputs
        self.add_input('a', 0.5, desc="Induced Velocity Factor")
        self.add_input('Area', 10.0, units="m**2", desc="Rotor disc area")
        self.add_input('rho', 1.225, units="kg/m**3", desc="air density")
        self.add_input('Vu', 10.0, units="m/s", desc="Freestream air velocity, upstream of rotor")

        # Outputs
        self.add_output('Vr', 0.0, units="m/s",
                        desc="Air velocity at rotor exit plane")
        self.add_output('Vd', 0.0, units="m/s",
                        desc="Slipstream air velocity, downstream of rotor")
        self.add_output('Ct', 0.0, desc="Thrust Coefficient")
        self.add_output('thrust', 0.0, units="N",
                        desc="Thrust produced by the rotor")
        self.add_output('Cp', 0.0, desc="Power Coefficient")
        self.add_output('power', 0.0, units="W", desc="Power produced by the rotor")

        # Every output depends on `a`
        self.declare_partials(of='*', wrt='a', method='cs')

        # Other dependencies
        self.declare_partials(of='Vr', wrt=['Vu'], method='cs')
        self.declare_partials(of=['thrust', 'power'], wrt=['Area', 'rho', 'Vu'], method='cs')

    def compute(self, inputs, outputs):
        """ Considering the entire rotor as a single disc that extracts
        velocity uniformly from the incoming flow and converts it to
        power."""

        a = inputs['a']
        Vu = inputs['Vu']

        qA = .5 * inputs['rho'] * inputs['Area'] * Vu ** 2

        outputs['Vd'] = Vd = Vu * (1 - 2 * a)
        outputs['Vr'] = .5 * (Vu + Vd)

        outputs['Ct'] = Ct = 4 * a * (1 - a)
        outputs['thrust'] = Ct * qA

        outputs['Cp'] = Cp = Ct * (1 - a)
        outputs['power'] = Cp * qA * Vu

Build the problem and add the actuator disc model

prob = om.Problem()
prob.model.add_subsystem('a_disk', ActuatorDisc(),
                         promotes_inputs=['a', 'Area', 'rho', 'Vu']);

Define the driver and optimization problem

prob.driver = om.ScipyOptimizeDriver()
prob.driver.options['optimizer'] = 'SLSQP'

prob.model.add_design_var('a', lower=0., upper=1.)

# negative one so we maximize the objective
prob.model.add_objective('a_disk.Cp', scaler=-1)

Call setup and provide the initial guess

prob.setup()

prob.set_val('a', .5)
prob.set_val('Area', 10.0, units='m**2')
prob.set_val('rho', 1.225, units='kg/m**3')
prob.set_val('Vu', 10.0, units='m/s')

Run the optimization

result = prob.run_driver()

Optimization terminated successfully    (Exit mode 0)
            Current function value: -0.592592590665925
            Iterations: 5
            Function evaluations: 6
            Gradient evaluations: 5
Optimization Complete
-----------------------------------

View the inputs and outputs

prob.model.list_inputs(val=True, units=True)

4 Input(s) in 'model'

varname  val           units    prom_name
-------  ------------  -------  ---------
a_disk
  a      [0.33335528]  None     a        
  Area   [10.]         m**2     Area     
  rho    [1.225]       kg/m**3  rho      
  Vu     [10.]         m/s      Vu       

[('a_disk.a', {'units': None, 'prom_name': 'a', 'val': array([0.33335528])}),
 ('a_disk.Area', {'units': 'm**2', 'prom_name': 'Area', 'val': array([10.])}),
 ('a_disk.rho',
  {'units': 'kg/m**3', 'prom_name': 'rho', 'val': array([1.225])}),
 ('a_disk.Vu', {'units': 'm/s', 'prom_name': 'Vu', 'val': array([10.])})]

prob.model.list_outputs(val=True, units=True)

6 Explicit Output(s) in 'model'

varname   val              units  prom_name    
--------  ---------------  -----  -------------
a_disk
  Vr      [6.6664472]      m/s    a_disk.Vr    
  Vd      [3.33289439]     m/s    a_disk.Vd    
  Ct      [0.88891815]     None   a_disk.Ct    
  thrust  [544.46236677]   N      a_disk.thrust
  Cp      [0.59259259]     None   a_disk.Cp    
  power   [3629.62961783]  W      a_disk.power 


0 Implicit Output(s) in 'model'

[('a_disk.Vr',
  {'units': 'm/s', 'val': array([6.6664472]), 'prom_name': 'a_disk.Vr'}),
 ('a_disk.Vd',
  {'units': 'm/s', 'val': array([3.33289439]), 'prom_name': 'a_disk.Vd'}),
 ('a_disk.Ct',
  {'units': None, 'val': array([0.88891815]), 'prom_name': 'a_disk.Ct'}),
 ('a_disk.thrust',
  {'units': 'N', 'val': array([544.46236677]), 'prom_name': 'a_disk.thrust'}),
 ('a_disk.Cp',
  {'units': None, 'val': array([0.59259259]), 'prom_name': 'a_disk.Cp'}),
 ('a_disk.power',
  {'units': 'W', 'val': array([3629.62961783]), 'prom_name': 'a_disk.power'})]

# Verify the correct outputs

# minimum value
print(prob.get_val('a_disk.Cp'))
print(prob.get_val('a'))

[0.59259259]
[0.33335528]