Building Models with Solvers and Implicit Components#
This tutorial will show you how to define implicit components and build models with them. We’ll use a nonlinear circuit analysis example problem.
Circuit analysis#
Consider a simple electrical circuit made up from two resistors, a diode, and a constant current source. Our goal is to solve for the steady-state voltages at node 1 and node 2.
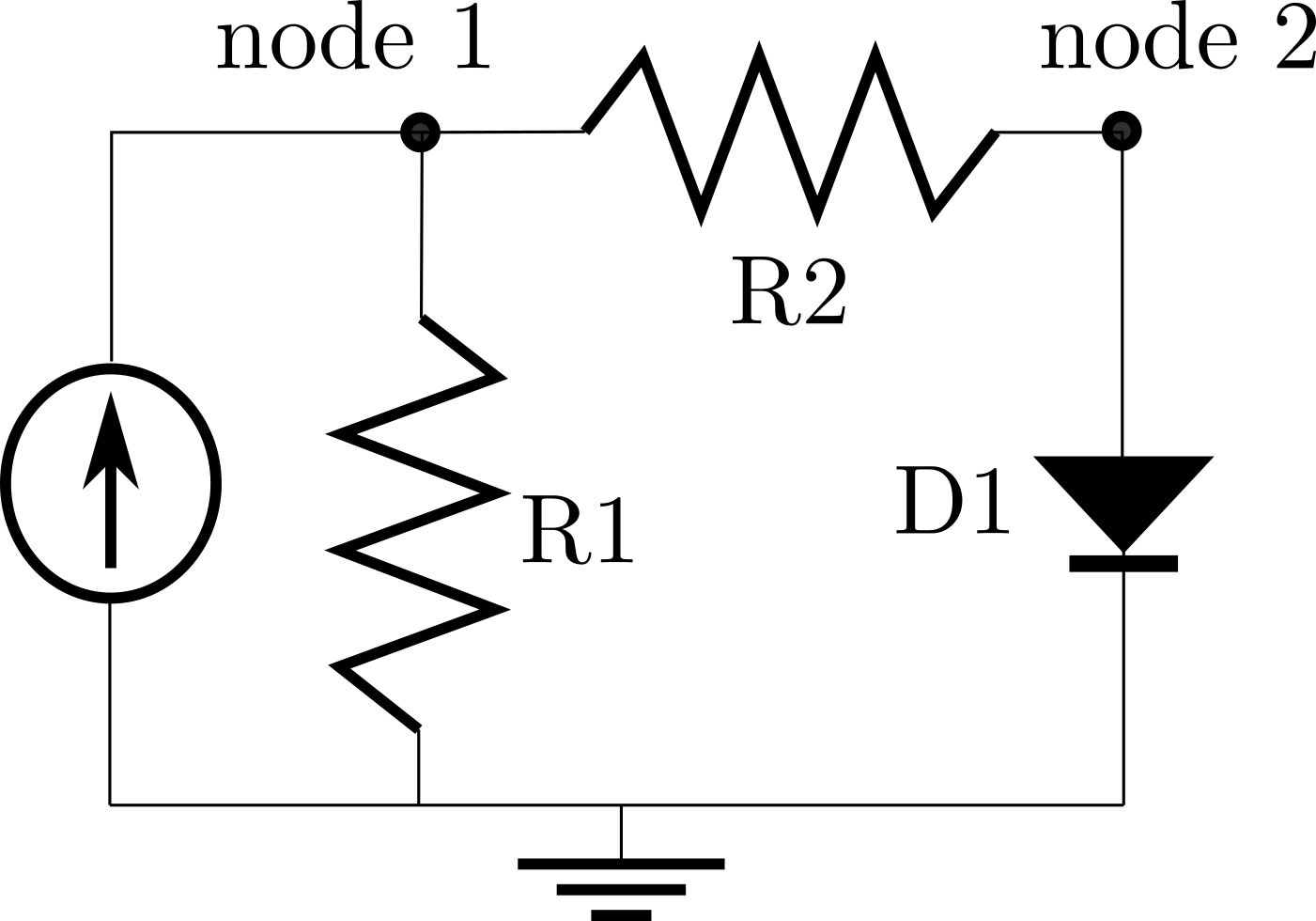
In order to find the voltages, we’ll employ Kirchoff’s current law, and solve for the voltages needed at each node to drive the net current to 0.
This means that the voltages at each node are state variables for the analysis. In other words, V1 and V2 are defined implicitly by the following residual equation:
\({R_{node_j}} = \sum_k I_{k}^{in} - \sum_k I_{k}^{out} = 0 .\)
To build this model we’re going to define three different components:
Resistor (Explicit)
Diode (Explicit)
Node (Implicit)
ExplicitComponents - Resistor and Diode
The Resistor and Diode components will each compute their current, given the voltages on either side.
These calculations are analytic functions, so we’ll inherit from ExplicitComponent. These components will each declare some options to allow you to pass in the relevant physical constants, and to allow you to give some reasonable default values.
import openmdao.api as om
class Resistor(om.ExplicitComponent):
"""Computes current across a resistor using Ohm's law."""
def initialize(self):
self.options.declare('R', default=1., desc='Resistance in Ohms')
def setup(self):
self.add_input('V_in', units='V')
self.add_input('V_out', units='V')
self.add_output('I', units='A')
def setup_partials(self):
self.declare_partials('I', 'V_in', method='fd')
self.declare_partials('I', 'V_out', method='fd')
def compute(self, inputs, outputs):
deltaV = inputs['V_in'] - inputs['V_out']
outputs['I'] = deltaV / self.options['R']
class Diode(om.ExplicitComponent):
"""Computes current across a diode using the Shockley diode equation."""
def initialize(self):
self.options.declare('Is', default=1e-15, desc='Saturation current in Amps')
self.options.declare('Vt', default=.025875, desc='Thermal voltage in Volts')
def setup(self):
self.add_input('V_in', units='V')
self.add_input('V_out', units='V')
self.add_output('I', units='A')
def setup_partials(self):
self.declare_partials('I', 'V_in', method='fd')
self.declare_partials('I', 'V_out', method='fd')
def compute(self, inputs, outputs):
deltaV = inputs['V_in'] - inputs['V_out']
Is = self.options['Is']
Vt = self.options['Vt']
outputs['I'] = Is * (np.exp(deltaV / Vt) - 1)
Important
Since we’ve provided default values for the options, they won’t be required arguments when instantiating Resistor or Diode. Check out the Features section for more details on how to use component options.
ImplicitComponent - Node#
The Node component inherits from ImplicitComponent, which has a different interface than ExplicitComponent.
Rather than compute the values of its outputs, it computes residuals via the apply_nonlinear method.
When those residuals have been driven to zero, the values of the outputs will be implicitly known.
apply_nonlinear computes the residuals using values from inputs and outputs.
Notice that we still define V as an output of the Node component, albeit one that is implicitly defined.
class Node(om.ImplicitComponent):
"""Computes voltage residual across a node based on incoming and outgoing current."""
def initialize(self):
self.options.declare('n_in', default=1, types=int, desc='number of connections with + assumed in')
self.options.declare('n_out', default=1, types=int, desc='number of current connections + assumed out')
def setup(self):
self.add_output('V', val=5., units='V')
for i in range(self.options['n_in']):
i_name = 'I_in:{}'.format(i)
self.add_input(i_name, units='A')
for i in range(self.options['n_out']):
i_name = 'I_out:{}'.format(i)
self.add_input(i_name, units='A')
def setup_partials(self):
#note: we don't declare any partials wrt `V` here,
# because the residual doesn't directly depend on it
self.declare_partials('V', 'I*', method='fd')
def apply_nonlinear(self, inputs, outputs, residuals):
residuals['V'] = 0.
for i_conn in range(self.options['n_in']):
residuals['V'] += inputs['I_in:{}'.format(i_conn)]
for i_conn in range(self.options['n_out']):
residuals['V'] -= inputs['I_out:{}'.format(i_conn)]
Every state variable must have exactly one corresponding residual which is defined in the apply_nonlinear method. The residuals equations in an implicit component are not analogous to the outputs equations in the compute method of an explicit component. Instead of defining an explicit equation for the output, residuals['example_output'] defines an equation for the residual associated with the output (state variable) example_output. In our example, residuals['V'] defines the equation of the residual associated with the state variable V. There will be no explicit
equation defining V, instead, the residual equation sums the currents associated with V so the sum can be driven to zero.
An implicit component varies its outputs (state variables, in this case V) to drive the residual equation to zero. In our model, V does not show up directly in the residual equation. Instead, our explicit components Resistor and Diode create a dependence of the currents on V, so by using a solver on a higher level of the model hierarchy, we can vary V to have an effect on current, and we can drive the residuals to zero.
All implicit components must define the apply_nonlinear method, but it is not a requirement that every ImplicitComponent define the solve_nonlinear method. (The solve_nonlinear method provides a way to explicitly define an output within an implicit component.) In fact, for the Node component, it is not even possible to define a solve_nonlinear because V does not show up directly in the residual function. So the implicit function represented by instances of the Node component must be converged at a higher level in the model hierarchy.
There are cases where it is possible, and even advantageous, to define the solve_nonlinear method.
For example, when a component is performing an engineering analysis with its own specialized nonlinear solver routines (e.g. CFD or FEM), then it makes sense to expose those to OpenMDAO via solve_nonlinear so OpenMDAO can make use of them. Just remember that apply_nonlinear must be defined, regardless of whether you also define solve_nonlinear.
Important
In this case, the residual equation is not a direct function of the state variable V. Often, however, the residual might be a direct function of one or more output variables. If that is the case, you can access the values via outputs['V']. See the ImplicitComponent documentation for an example of this.
Building the Circuit Group and Solving It with NewtonSolver#
We can combine the Resistor, Diode, and Node into the circuit pictured above using a Group. Adding components and connecting their variables is the same as what you’ve seen before in the Sellar - Two Discipline tutorial. What is new here is the additional use of the nonlinear NewtonSolver and linear DirectSolver to converge the system.
In previous tutorials, we used a gradient-free NonlinearBlockGaussSeidel solver, but that won’t work here. Just above, we discussed that the Node class does not, and in fact can not, define its own solve_nonlinear method. Hence, there would be no calculations for the GaussSeidel solver to iterate on.
Instead we use the Newton solver at the Circuit level, which uses Jacobian information to compute group level updates for all the variables simultaneously. The Newton solver’s use of that Jacobian information is why we need to declare a linear solver in this case.
Important
OpenMDAO provides a library of linear solvers that are useful in different advanced scenarios. For many problems, especially problems built from components with mostly scalar variables, the DirectSolver will be both the most efficient and the easiest to use. We recommend you stick with DirectSolver unless you have a good reason to switch.
import numpy as np
class Circuit(om.Group):
def setup(self):
self.add_subsystem('n1', Node(n_in=1, n_out=2), promotes_inputs=[('I_in:0', 'I_in')])
self.add_subsystem('n2', Node()) # leaving defaults
self.add_subsystem('R1', Resistor(R=100.), promotes_inputs=[('V_out', 'Vg')])
self.add_subsystem('R2', Resistor(R=10000.))
self.add_subsystem('D1', Diode(), promotes_inputs=[('V_out', 'Vg')])
self.connect('n1.V', ['R1.V_in', 'R2.V_in'])
self.connect('R1.I', 'n1.I_out:0')
self.connect('R2.I', 'n1.I_out:1')
self.connect('n2.V', ['R2.V_out', 'D1.V_in'])
self.connect('R2.I', 'n2.I_in:0')
self.connect('D1.I', 'n2.I_out:0')
self.nonlinear_solver = om.NewtonSolver(solve_subsystems=False)
self.nonlinear_solver.options['iprint'] = 2
self.nonlinear_solver.options['maxiter'] = 20
self.linear_solver = om.DirectSolver()
p = om.Problem()
model = p.model
model.add_subsystem('ground', om.IndepVarComp('V', 0., units='V'))
model.add_subsystem('source', om.IndepVarComp('I', 0.1, units='A'))
model.add_subsystem('circuit', Circuit())
model.connect('source.I', 'circuit.I_in')
model.connect('ground.V', 'circuit.Vg')
p.setup()
# set some initial guesses
p['circuit.n1.V'] = 10.
p['circuit.n2.V'] = 1.
p.run_model()
print(p['circuit.n1.V'])
print(p['circuit.n2.V'])
print(p['circuit.R1.I'])
print(p['circuit.R2.I'])
print(p['circuit.D1.I'])
# sanity check: should sum to .1 Amps
print(p['circuit.R1.I'] + p['circuit.D1.I'])
=======
circuit
=======
NL: Newton 0 ; 59.9046598 1
NL: Newton 1 ; 22.3887968 0.373740489
NL: Newton 2 ; 8.23629948 0.13749013
NL: Newton 3 ; 3.02978539 0.0505767899
NL: Newton 4 ; 1.11437824 0.0186025301
NL: Newton 5 ; 0.409725119 0.00683962016
NL: Newton 6 ; 0.150492273 0.00251219644
NL: Newton 7 ; 0.0551239641 0.000920194929
NL: Newton 8 ; 0.0200403261 0.000334537016
NL: Newton 9 ; 0.00713760492 0.000119149411
NL: Newton 10 ; 0.00240281896 4.01107188e-05
NL: Newton 11 ; 0.000692025598 1.15521163e-05
NL: Newton 12 ; 0.000129140479 2.15576685e-06
NL: Newton 13 ; 7.60315074e-06 1.26920857e-07
NL: Newton 14 ; 3.10658294e-08 5.18587861e-10
NL: Newton 15 ; 1.12045627e-12 1.87039918e-14
NL: Newton Converged
[9.90804735]
[0.71278185]
[0.09908047]
[0.00091953]
[0.00091953]
[0.1]
Modifying Solver Settings in Your Run Script#
In the above run script, we set some initial guess values: prob['n1.V']=10 and prob['n2.V']=1.
If you try to play around with those initial guesses a bit, you will see that convergence is really sensitive to
the initial guess you used for n2.V.Below we provide a second run script that uses the same Circuit group we defined previously, but which additionally modifies some solver settings and initial guesses. If we set the initial guess for prob['n2.V']=1e-3, then the model starts out with a massive residual. It also converges much more slowly, so although we gave it more than twice the number of iterations, it doesn’t even get close to a converged answer.
from openmdao.test_suite.scripts.circuit_analysis import Circuit
p = om.Problem()
model = p.model
model.add_subsystem('ground', om.IndepVarComp('V', 0., units='V'))
model.add_subsystem('source', om.IndepVarComp('I', 0.1, units='A'))
model.add_subsystem('circuit', Circuit())
model.connect('source.I', 'circuit.I_in')
model.connect('ground.V', 'circuit.Vg')
p.setup()
# you can change the NewtonSolver settings in circuit after setup is called
newton = p.model.circuit.nonlinear_solver
newton.options['maxiter'] = 50
# set some initial guesses
p['circuit.n1.V'] = 10.
p['circuit.n2.V'] = 1e-3
p.run_model()
print(p['circuit.n1.V'])
print(p['circuit.n2.V'])
# sanity check: should sum to .1 Amps
print(p['circuit.R1.I'] + p['circuit.D1.I'])
=======
circuit
=======
NL: Newton 0 ; 2.53337743 1
NL: Newton 1 ; 6.9707252e+152 2.75155416e+152
NL: Newton 2 ; 2.56438649e+152 1.01224021e+152
NL: Newton 3 ; 9.43385069e+151 3.72382361e+151
NL: Newton 4 ; 3.47051972e+151 1.36991815e+151
NL: Newton 5 ; 1.27673286e+151 5.03964723e+150
NL: Newton 6 ; 4.69683769e+150 1.85398261e+150
NL: Newton 7 ; 1.72787003e+150 6.82042086e+149
NL: Newton 8 ; 6.35647859e+149 2.50909261e+149
NL: Newton 9 ; 2.33841779e+149 9.23043588e+148
NL: Newton 10 ; 8.60255831e+148 3.39568759e+148
NL: Newton 11 ; 3.16470434e+148 1.24920365e+148
NL: Newton 12 ; 1.16422967e+148 4.59556342e+147
NL: Newton 13 ; 4.28296159e+147 1.6906133e+147
NL: Newton 14 ; 1.57561352e+147 6.21941878e+146
NL: Newton 15 ; 5.79635819e+146 2.2879963e+146
NL: Newton 16 ; 2.13236101e+146 8.41706802e+145
NL: Newton 17 ; 7.84451778e+145 3.09646628e+145
NL: Newton 18 ; 2.88583682e+145 1.13912628e+145
NL: Newton 19 ; 1.06164004e+145 4.19061141e+144
NL: Newton 20 ; 3.90555543e+144 1.54163978e+144
NL: Newton 21 ; 1.43677355e+144 5.67137582e+143
NL: Newton 22 ; 5.2855945e+143 2.08638257e+143
NL: Newton 23 ; 1.94446155e+143 7.67537253e+142
NL: Newton 24 ; 7.15327429e+142 2.82361176e+142
NL: Newton 25 ; 2.63154255e+142 1.03874871e+142
NL: Newton 26 ; 9.68090402e+141 3.82134297e+141
NL: Newton 27 ; 3.56140556e+141 1.40579352e+141
NL: Newton 28 ; 1.31016789e+141 5.17162533e+140
NL: Newton 29 ; 4.81983831e+140 1.90253464e+140
NL: Newton 30 ; 1.77311942e+140 6.99903379e+139
NL: Newton 31 ; 6.52294182e+139 2.57480064e+139
NL: Newton 32 ; 2.39965619e+139 9.4721622e+138
NL: Newton 33 ; 8.82784179e+138 3.48461374e+138
NL: Newton 34 ; 3.2475815e+138 1.28191775e+138
NL: Newton 35 ; 1.19471847e+138 4.71591187e+137
NL: Newton 36 ; 4.39512363e+137 1.73488702e+137
NL: Newton 37 ; 1.61687562e+137 6.38229269e+136
NL: Newton 38 ; 5.94815301e+136 2.34791427e+136
NL: Newton 39 ; 2.18820321e+136 8.63749388e+135
NL: Newton 40 ; 8.04994972e+135 3.17755642e+135
NL: Newton 41 ; 2.96141101e+135 1.16895768e+135
NL: Newton 42 ; 1.08944223e+135 4.30035499e+134
NL: Newton 43 ; 4.00783397e+134 1.58201219e+134
NL: Newton 44 ; 1.47439972e+134 5.8198976e+133
NL: Newton 45 ; 5.42401346e+133 2.14102068e+133
NL: Newton 46 ; 1.99538304e+133 7.8763749e+132
NL: Newton 47 ; 7.34060398e+132 2.8975564e+132
NL: Newton 48 ; 2.70045729e+132 1.06595143e+132
NL: Newton 49 ; 9.93442718e+131 3.92141616e+131
NL: Newton 50 ; 3.65467152e+131 1.44260838e+131
NL: NewtonSolver 'NL: Newton' on system 'circuit' failed to converge in 50 iterations.
[9.98744678]
[8.732125]
[0.09987447]
Important
You actually can get this model to converge. But you have to set the options for maxiter=400 and rtol=1e-100. (The rtol value needs to be very low to prevent premature termination.)
Tweaking Newton Solver Settings to Get More Robust Convergence#
The NewtonSolver has a lot of features that allow you to modify its behavior to handle more challenging problems. We’re going to look at two of the most important ones here:
The solve_subsystems option
If we use both of these in combination, we can dramatically improve the robustness of the solver for this problem.
The linesearch attribute makes sure that the solver doesn’t take too big of a step. The solve_subsystems option allows the Resistor and Diode components (the two ExplicitComponents) to help the convergence by updating their own output values given their inputs. When you use NewtonSolver on models with a lot of ExplicitComponents, you may find that turning on solve_subsystems helps convergence, but you need to be careful about the execution order when you try this.
Important
For this case, we used the ArmijoGoldsteinLS, which basically limits step sizes so that the residual always goes down. For many problems you might want to use BoundsEnforceLS instead, which only activates the line search to enforce upper and lower bounds on the outputs in the model.
p = om.Problem()
model = p.model
model.add_subsystem('ground', om.IndepVarComp('V', 0., units='V'))
model.add_subsystem('source', om.IndepVarComp('I', 0.1, units='A'))
model.add_subsystem('circuit', Circuit())
model.connect('source.I', 'circuit.I_in')
model.connect('ground.V', 'circuit.Vg')
p.setup()
# you can change the NewtonSolver settings in circuit after setup is called
newton = p.model.circuit.nonlinear_solver
newton.options['iprint'] = 2
newton.options['maxiter'] = 10
newton.options['solve_subsystems'] = True
newton.linesearch = om.ArmijoGoldsteinLS()
newton.linesearch.options['maxiter'] = 10
newton.linesearch.options['iprint'] = 2
# set some initial guesses
p['circuit.n1.V'] = 10.
p['circuit.n2.V'] = 1e-3
p.run_model()
print(p['circuit.n1.V'])
print(p['circuit.n2.V'])
print(p['circuit.R1.I'])
print(p['circuit.R2.I'])
print(p['circuit.D1.I'])
# sanity check: should sum to .1 Amps
print(p['circuit.R1.I'] + p['circuit.D1.I'])
=======
circuit
=======
NL: Newton 0 ; 0.00141407214 1
| LS: AG 1 ; 6.9707252e+152 1
| LS: AG 2 ; 8.51199079e+68 0.5
| LS: AG 3 ; 9.40605982e+26 0.25
| LS: AG 4 ; 988771.709 0.125
| LS: AG 5 ; 0.00130322117 0.0625
NL: Newton 1 ; 0.00130322117 0.921608691
| LS: AG 1 ; 5580826.07 1
| LS: AG 2 ; 13.3748871 0.5
| LS: AG 3 ; 0.0198015756 0.25
| LS: AG 4 ; 0.000828003297 0.125
NL: Newton 2 ; 0.000828003297 0.585545301
NL: Newton 3 ; 7.02986117e-06 0.00497135964
NL: Newton 4 ; 2.64550002e-08 1.87083809e-05
NL: Newton 5 ; 3.78431444e-13 2.67618202e-10
NL: Newton Converged
[9.90804735]
[0.71278185]
[0.09908047]
[0.00091953]
[0.00091953]
[0.1]
Important
This tutorial used finite difference to approximate the partial derivatives for all the components. Check out this example if you want to see the same problem solved with analytic derivatives.
