BoundsEnforceLS

BoundsEnforceLS#

The BoundsEnforceLS only backtracks until variables violate their upper and lower bounds.

Here is a simple example where BoundsEnforceLS is used to backtrack during the Newton solver’s iteration on a system that contains an implicit component with 3 states that are confined to a small range of values.

ImplCompTwoStatesArrays class definition

class ImplCompTwoStatesArrays(om.ImplicitComponent):
    """
    A Simple Implicit Component with an additional output equation.

    f(x,z) = xz + z - 4
    y = x + 2z

    Sol : when x = 0.5, z = 2.666
    Sol : when x = 2.0, z = 1.333

    Coupled derivs:

    y = x + 8/(x+1)
    dy_dx = 1 - 8/(x+1)**2 = -2.5555555555555554

    z = 4/(x+1)
    dz_dx = -4/(x+1)**2 = -1.7777777777777777
    """

    def setup(self):
        self.add_input('x', np.zeros((3, 1)))
        self.add_output('y', np.zeros((3, 1)))
        self.add_output('z', 2.0*np.ones((3, 1)), lower=1.5,
            upper=np.array([2.6, 2.5, 2.65]).reshape((3,1)))

        self.maxiter = 10
        self.atol = 1.0e-12

    def setup_partials(self):
        self.declare_partials(of='*', wrt='*')

    def apply_nonlinear(self, inputs, outputs, residuals):
        """
        Don't solve; just calculate the residual.
        """

        x = inputs['x']
        y = outputs['y']
        z = outputs['z']

        residuals['y'] = y - x - 2.0*z
        residuals['z'] = x*z + z - 4.0

    def linearize(self, inputs, outputs, jac):
        """
        Analytical derivatives.
        """

        # Output equation
        jac[('y', 'x')] = -np.diag(np.array([1.0, 1.0, 1.0]))
        jac[('y', 'y')] = np.diag(np.array([1.0, 1.0, 1.0]))
        jac[('y', 'z')] = -np.diag(np.array([2.0, 2.0, 2.0]))

        # State equation
        jac[('z', 'z')] = (inputs['x'] + 1.0) * np.eye(3)
        jac[('z', 'x')] = outputs['z'] * np.eye(3)

import numpy as np

import openmdao.api as om
from openmdao.test_suite.components.implicit_newton_linesearch import ImplCompTwoStatesArrays

top = om.Problem()
top.model.add_subsystem('comp', ImplCompTwoStatesArrays(), promotes_inputs=['x'])

top.model.nonlinear_solver = om.NewtonSolver(solve_subsystems=False)
top.model.nonlinear_solver.options['maxiter'] = 10
top.model.linear_solver = om.ScipyKrylov()

top.model.nonlinear_solver.linesearch = om.BoundsEnforceLS()

top.setup()
top.set_val('x', np.array([2., 2, 2]).reshape(3, 1))

# Test lower bounds: should go to the lower bound and stall
top.set_val('comp.y', 0.)
top.set_val('comp.z', 1.6)
top.run_model()

for ind in range(3):
    print(top.get_val('comp.z', indices=ind))

NL: NewtonSolver 'NL: Newton' on system '' failed to converge in 10 iterations.
[1.5]
[1.5]
[1.5]

BoundsEnforceLS Options#

Option	Default	Acceptable Values	Acceptable Types	Description
bound_enforcement	scalar	['vector', 'scalar', 'wall']	N/A	If this is set to 'vector', the entire vector is backtracked together when a bound is violated. If this is set to 'scalar', only the violating entries are set to the bound and then the backtracking occurs on the vector as a whole. If this is set to 'wall', only the violating entries are set to the bound, and then the backtracking follows the wall - i.e., the violating entries do not change during the line search.
debug_print	False	[True, False]	['bool']	If true, the values of input and output variables at the start of iteration are printed and written to a file after a failure to converge.
iprint	1	N/A	['int']	whether to print output
print_bound_enforce	False	N/A	N/A	Set to True to print out names and values of variables that are pulled back to their bounds.
stall_limit	0	N/A	N/A	Number of iterations after which, if the residual norms are identical within the stall_tol, then terminate as if max iterations were reached. Default is 0, which disables this feature.
stall_tol	1e-12	N/A	N/A	When stall checking is enabled, the threshold below which the residual norm is considered unchanged.
stall_tol_type	rel	['abs', 'rel']	N/A	Specifies whether the absolute or relative norm of the residual is used for stall detection.

BoundsEnforceLS Constructor#

The call signature for the BoundsEnforceLS constructor is:

BoundsEnforceLS.__init__(**kwargs)

Initialize all attributes.

Parameters:

**kwargsdict
Options dictionary.

BoundsEnforceLS Option Examples#

bound_enforcement

BoundsEnforceLS includes the bound_enforcement option in its options dictionary. This option has a dual role:

Behavior of the non-bounded variables when the bounded ones are capped.
Direction of the further backtracking.

There are three difference bounds enforcement schemes available in this option.

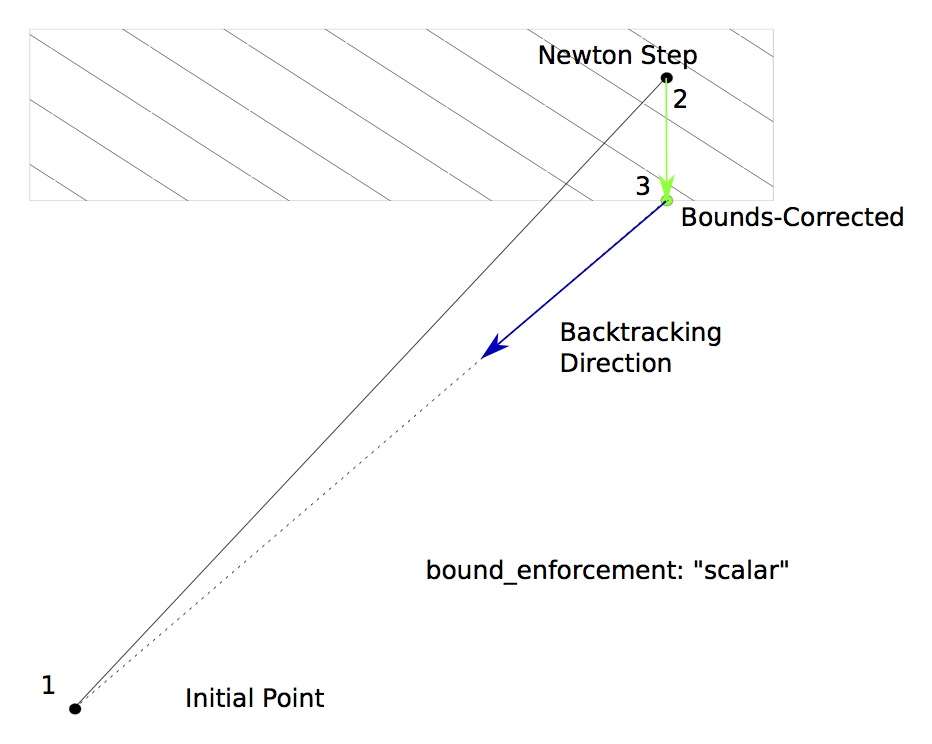
With “scalar” bounds enforcement, only the variables that violate their bounds are pulled back to feasible values; the remaining values are kept at the Newton-stepped point. This changes the direction of the backtracking vector so that it still moves in the direction of the initial point. This is the default bounds enforcement for BoundsEnforceLS.

BT2

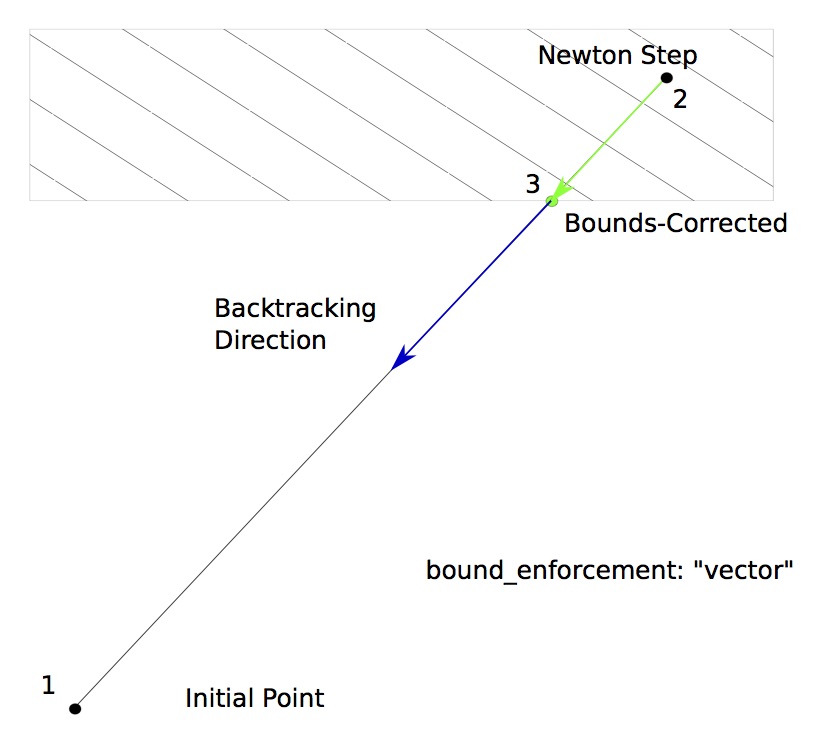
With “vector” bounds enforcement, the solution in the output vector is pulled back in unison to a point where none of the variables violate any upper or lower bounds. Further backtracking continues along the Newton gradient direction vector back towards the initial point.

BT1

With “wall” bounds enforcement, only the variables that violate their bounds are pulled back to feasible values; the remaining values are kept at the Newton-stepped point. Further backtracking only occurs in the direction of the non-violating variables, so that it will move along the wall.

Note

When using BoundsEnforceLS linesearch, the scalar and wall methods are exactly the same because no further backtracking is performed.

BT3

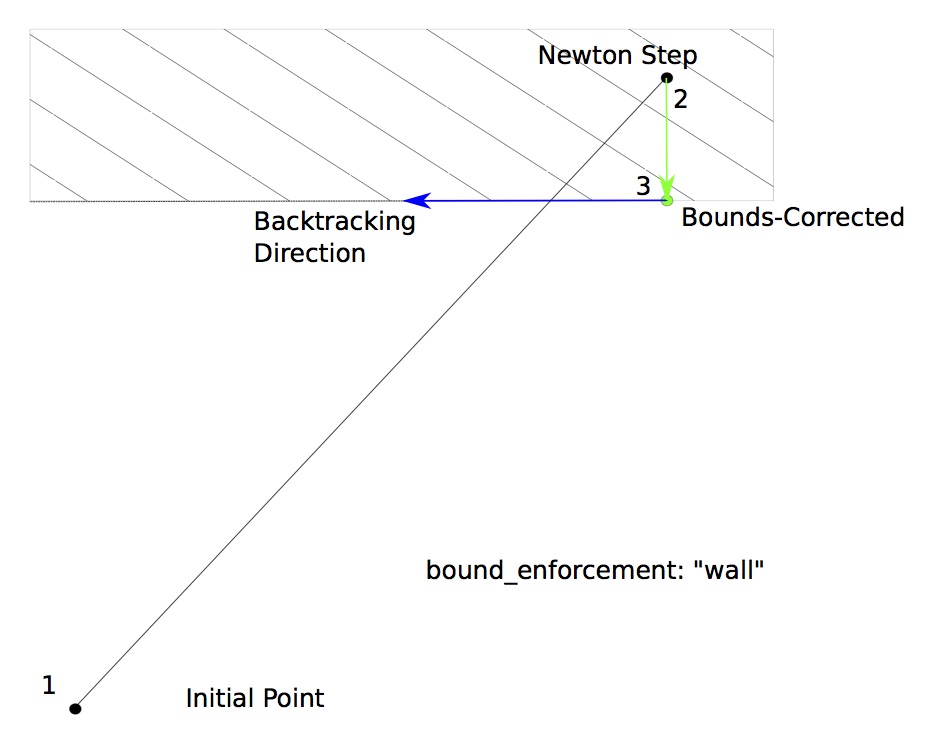
Here are a few examples of this option:

bound_enforcement: vector

The bound_enforcement option in the options dictionary is used to specify how the output bounds are enforced. When this is set to “vector”, the output vector is rolled back along the computed gradient until it reaches a point where the earliest bound violation occurred. The backtracking continues along the original computed gradient.

from openmdao.test_suite.components.implicit_newton_linesearch import ImplCompTwoStatesArrays

top = om.Problem()
top.model.add_subsystem('comp', ImplCompTwoStatesArrays(), promotes_inputs=['x'])

top.model.nonlinear_solver = om.NewtonSolver(solve_subsystems=False)
top.model.nonlinear_solver.options['maxiter'] = 10
top.model.linear_solver = om.ScipyKrylov()

top.model.nonlinear_solver.linesearch = om.BoundsEnforceLS(bound_enforcement='vector')

top.setup()
top.set_val('x', np.array([2., 2, 2]).reshape(3, 1))

# Test lower bounds: should go to the lower bound and stall
top.set_val('comp.y', 0.)
top.set_val('comp.z', 1.6)
top.run_model()

for ind in range(3):
    print(top.get_val('comp.z', indices=ind))

NL: NewtonSolver 'NL: Newton' on system '' failed to converge in 10 iterations.
[1.5]
[1.5]
[1.5]

bound_enforcement: scalar

The bound_enforcement option in the options dictionary is used to specify how the output bounds are enforced. When this is set to “scaler”, then the only indices in the output vector that are rolled back are the ones that violate their upper or lower bounds. The backtracking continues along the modified gradient.

from openmdao.test_suite.components.implicit_newton_linesearch import ImplCompTwoStatesArrays

top = om.Problem()
top.model.add_subsystem('comp', ImplCompTwoStatesArrays(), promotes_inputs=['x'])

top.model.nonlinear_solver = om.NewtonSolver(solve_subsystems=False)
top.model.nonlinear_solver.options['maxiter'] = 10
top.model.linear_solver = om.ScipyKrylov()

top.model.nonlinear_solver.linesearch = om.BoundsEnforceLS(bound_enforcement='scalar')

top.setup()
top.set_val('x', np.array([2., 2, 2]).reshape(3, 1))
top.run_model()

NL: NewtonSolver 'NL: Newton' on system '' failed to converge in 10 iterations.

# Test lower bounds: should stop just short of the lower bound
top.set_val('comp.y', 0.)
top.set_val('comp.z', 1.6)
top.run_model()

NL: NewtonSolver 'NL: Newton' on system '' failed to converge in 10 iterations.

bound_enforcement: wall

The bound_enforcement option in the options dictionary is used to specify how the output bounds are enforced. When this is set to “wall”, then the only indices in the output vector that are rolled back are the ones that violate their upper or lower bounds. The backtracking continues along a modified gradient direction that follows the boundary of the violated output bounds.

from openmdao.test_suite.components.implicit_newton_linesearch import ImplCompTwoStatesArrays

top = om.Problem()
top.model.add_subsystem('comp', ImplCompTwoStatesArrays(), promotes_inputs=['x'])

top.model.nonlinear_solver = om.NewtonSolver(solve_subsystems=False)
top.model.nonlinear_solver.options['maxiter'] = 10
top.model.linear_solver = om.ScipyKrylov()

top.model.nonlinear_solver.linesearch = om.BoundsEnforceLS(bound_enforcement='wall')

top.setup()
top.set_val('x', np.array([0.5, 0.5, 0.5]).reshape(3, 1))

# Test upper bounds: should go to the upper bound and stall
top.set_val('comp.y', 0.)
top.set_val('comp.z', 2.4)
top.run_model()

print(top.get_val('comp.z', indices=0))
print(top.get_val('comp.z', indices=1))
print(top.get_val('comp.z', indices=2))

NL: NewtonSolver 'NL: Newton' on system '' failed to converge in 10 iterations.
[2.6]
[2.5]
[2.65]

BoundsEnforceLS

Contents

BoundsEnforceLS#

BoundsEnforceLS Options#

BoundsEnforceLS Constructor#

BoundsEnforceLS Option Examples#