In the previous tutorial , we built up a model of an electrical circuit using a combination of ImplicitComponent and ExplicitComponent instances.In that tutorial, all of the implicit relationships in the model came directly from the physics of the model itself.
However, you often need to add implicit relationships to models by driving the values of two separate variables to be equal to each other. In this tutorial, we’ll show you how to do that using the BalanceComp.
Using BalanceComp to Create Implicit Relationships in Groups#
The electrical circuit model from the previous tutorial represents a very basic circuit with a current source of .1 Amps. Here is a reminder of what that circuit looked like:
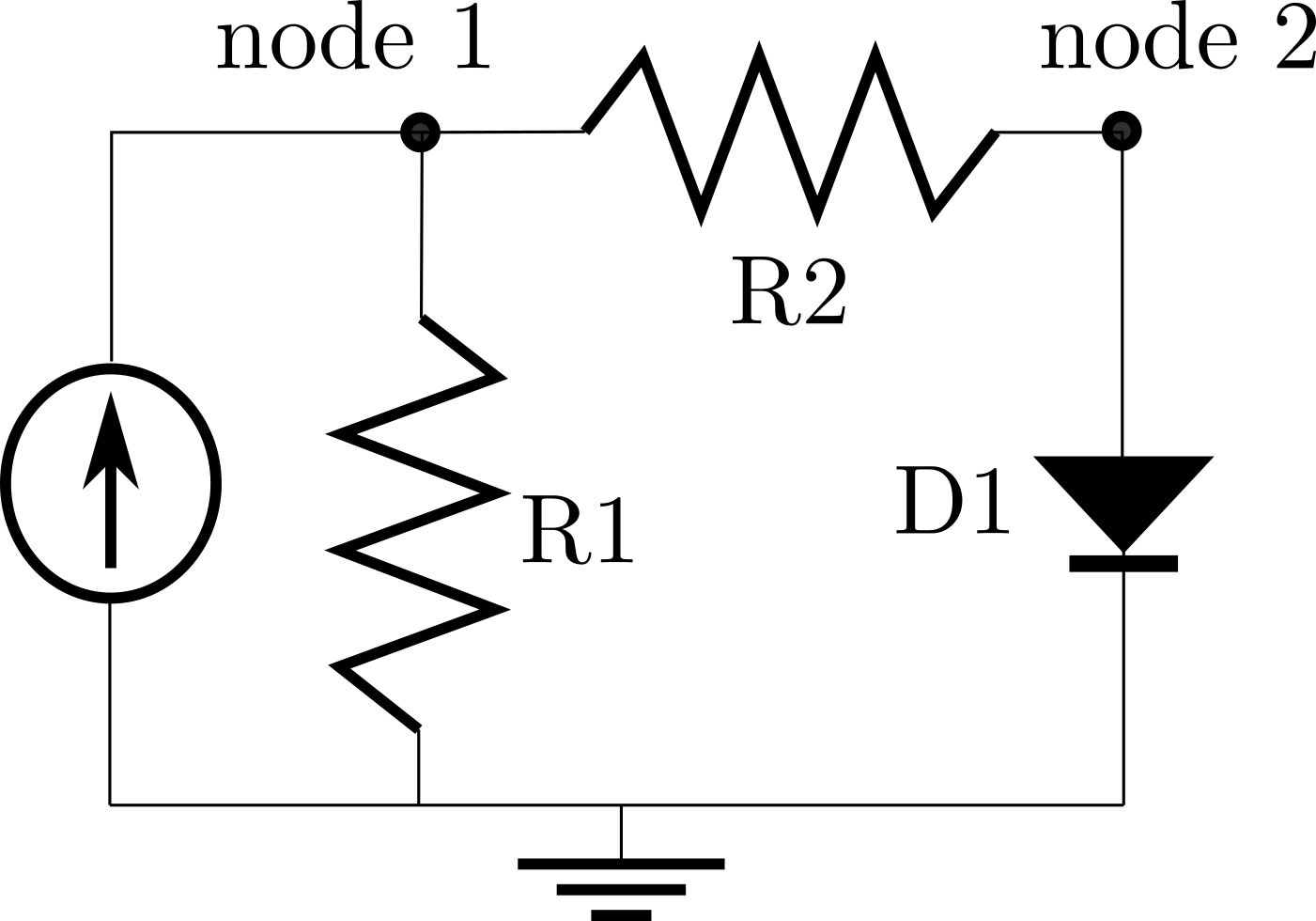
When we solved that circuit, the resulting voltage at node 1 was 9.9 Volts. Let’s say you wanted to power this circuit with a 1.5-Volt battery, instead of using a current source. We can make a small modification to our original model to capture this new setup.
Given any value for source.I, this model outputs the value for n1.V that balances the model. The voltage at the ground is also known via ground.V. So the voltage across the current source is
To represent a voltage source with a specific voltage, we can add an additional state variable and residual equation to our model:
where \(V_{source}^{*}\), the desired source voltage, is given by the user as parameter to the model.
We could write a new component, inheriting from ImplicitComponent, to include this new relationship into the model, but OpenMDAO provides BalanceComp, a general utility component that is designed specifically for this type of situation.
What we’re going to do is add a BalanceComp to the top level of the model.
The BalanceComp will define a residual that will drive the source current to force the delta-V across the battery to be what we want. We’ll also add an ExecComp to compute that delta-V from the ground voltage and the voltage at node 1 and then connect everything up. Lastly, since we added an ImplicitComponent at the top level of the model, we’ll also move the NewtonSolver up to the top level of the model, too.
Important
BalanceComp can handle more than just \(lhs-rhs=0\). It has a number of inputs that let you tweak that behavior. It can support multiple residuals and array variables as well. Check out the documentation on it for details.
Circuit class definition
class Circuit(om.Group):
def setup(self):
self.add_subsystem('n1', Node(n_in=1, n_out=2), promotes_inputs=[('I_in:0', 'I_in')])
self.add_subsystem('n2', Node()) # leaving defaults
self.add_subsystem('R1', Resistor(R=100.), promotes_inputs=[('V_out', 'Vg')])
self.add_subsystem('R2', Resistor(R=10000.))
self.add_subsystem('D1', Diode(), promotes_inputs=[('V_out', 'Vg')])
self.connect('n1.V', ['R1.V_in', 'R2.V_in'])
self.connect('R1.I', 'n1.I_out:0')
self.connect('R2.I', 'n1.I_out:1')
self.connect('n2.V', ['R2.V_out', 'D1.V_in'])
self.connect('R2.I', 'n2.I_in:0')
self.connect('D1.I', 'n2.I_out:0')
self.nonlinear_solver = om.NewtonSolver(solve_subsystems=False)
self.nonlinear_solver.options['iprint'] = 2
self.nonlinear_solver.options['maxiter'] = 20
self.linear_solver = om.DirectSolver()
import openmdao.api as om
from openmdao.test_suite.scripts.circuit_analysis import Circuit
p = om.Problem()
model = p.model
model.add_subsystem('ground', om.IndepVarComp('V', 0., units='V'))
# replacing the fixed current source with a BalanceComp to represent a fixed Voltage source
# model.add_subsystem('source', om.IndepVarComp('I', 0.1, units='A'))
model.add_subsystem('batt', om.IndepVarComp('V', 1.5, units='V'))
bal = model.add_subsystem('batt_balance', om.BalanceComp())
bal.add_balance('I', units='A', eq_units='V')
model.add_subsystem('circuit', Circuit())
model.add_subsystem('batt_deltaV', om.ExecComp('dV = V1 - V2', V1={'units':'V'},
V2={'units':'V'}, dV={'units':'V'}))
# current into the circuit is now the output state from the batt_balance comp
model.connect('batt_balance.I', 'circuit.I_in')
model.connect('ground.V', ['circuit.Vg','batt_deltaV.V2'])
model.connect('circuit.n1.V', 'batt_deltaV.V1')
# set the lhs and rhs for the battery residual
model.connect('batt.V', 'batt_balance.rhs:I')
model.connect('batt_deltaV.dV', 'batt_balance.lhs:I')
p.setup()
###################
# Solver Setup
###################
# change the circuit solver to RunOnce because we're
# going to converge at the top level of the model with newton instead
p.model.circuit.nonlinear_solver = om.NonlinearRunOnce()
p.model.circuit.linear_solver = om.LinearRunOnce()
# Put Newton at the top so it can also converge the new BalanceComp residual
newton = p.model.nonlinear_solver = om.NewtonSolver()
p.model.linear_solver = om.DirectSolver()
newton.options['iprint'] = 2
newton.options['maxiter'] = 20
newton.options['solve_subsystems'] = True
newton.linesearch = om.ArmijoGoldsteinLS()
newton.linesearch.options['maxiter'] = 10
newton.linesearch.options['iprint'] = 2
# set initial guesses from the current source problem
p['circuit.n1.V'] = 9.8
p['circuit.n2.V'] = .7
p.run_model()
print(p['circuit.n1.V'])
print(p['circuit.n2.V'])
print(p['circuit.R1.I'])
print(p['circuit.R2.I'])
print(p['circuit.D1.I'])
NL: Newton 0 ; 5.38788524 1
NL: Newton 1 ; 0.000156774226 2.90975437e-05
NL: Newton 2 ; 4.09995323e-05 7.60957788e-06
NL: Newton 3 ; 5.81925105e-06 1.08006217e-06
NL: Newton 4 ; 1.73138595e-07 3.21347964e-08
NL: Newton 5 ; 1.65860813e-10 3.07840285e-11
NL: Newton Converged
[1.5]
[0.65113362]
[0.015]
[8.48866377e-05]
[8.48868035e-05]
Understanding How Everything Is Connected in This Model#
There are a number of connections in this model, and several different residuals being converged. Trying to keep track of all the connections in your head can be a bit challenging, but OpenMDAO offers some visualization tools to help see what’s going on.
The openmdao n2 command can be used to view an \(N^2\) diagram of the model. It can be used
as follows:
openmdao n2 <your_python_script>
You can do the same thing programmatically by calling the n2 function in your python script (after setup):
p.setup()
om.n2(p)
Here is what the resulting visualization would look like for the above model:
