ArmijoGoldsteinLS

ArmijoGoldsteinLS#

ArmijoGoldsteinLS checks bounds and backtracks to a point that satisfies them. From there, further backtracking is performed, until the termination criteria are satisfied. The main termination criteria is the Armijo-Goldstein condition, which checks for a sufficient decrease from the initial point by measuring the slope. There is also an iteration maximum.

Here is a simple example where ArmijoGoldsteinLS is used to backtrack during the Newton solver’s iteration on a system that contains an implicit component with 3 states that are confined to a small range of values.

ImplCompTwoStatesArrays class definition

class ImplCompTwoStatesArrays(om.ImplicitComponent):
    """
    A Simple Implicit Component with an additional output equation.

    f(x,z) = xz + z - 4
    y = x + 2z

    Sol : when x = 0.5, z = 2.666
    Sol : when x = 2.0, z = 1.333

    Coupled derivs:

    y = x + 8/(x+1)
    dy_dx = 1 - 8/(x+1)**2 = -2.5555555555555554

    z = 4/(x+1)
    dz_dx = -4/(x+1)**2 = -1.7777777777777777
    """

    def setup(self):
        self.add_input('x', np.zeros((3, 1)))
        self.add_output('y', np.zeros((3, 1)))
        self.add_output('z', 2.0*np.ones((3, 1)), lower=1.5,
            upper=np.array([2.6, 2.5, 2.65]).reshape((3,1)))

        self.maxiter = 10
        self.atol = 1.0e-12

    def setup_partials(self):
        self.declare_partials(of='*', wrt='*')

    def apply_nonlinear(self, inputs, outputs, residuals):
        """
        Don't solve; just calculate the residual.
        """

        x = inputs['x']
        y = outputs['y']
        z = outputs['z']

        residuals['y'] = y - x - 2.0*z
        residuals['z'] = x*z + z - 4.0

    def linearize(self, inputs, outputs, jac):
        """
        Analytical derivatives.
        """

        # Output equation
        jac[('y', 'x')] = -np.diag(np.array([1.0, 1.0, 1.0]))
        jac[('y', 'y')] = np.diag(np.array([1.0, 1.0, 1.0]))
        jac[('y', 'z')] = -np.diag(np.array([2.0, 2.0, 2.0]))

        # State equation
        jac[('z', 'z')] = (inputs['x'] + 1.0) * np.eye(3)
        jac[('z', 'x')] = outputs['z'] * np.eye(3)

import numpy as np
import openmdao.api as om

from openmdao.test_suite.components.implicit_newton_linesearch import ImplCompTwoStatesArrays

top = om.Problem()
top.model.add_subsystem('comp', ImplCompTwoStatesArrays(), promotes_inputs=['x'])

top.model.nonlinear_solver = om.NewtonSolver(solve_subsystems=False)
top.model.nonlinear_solver.options['maxiter'] = 10
top.model.linear_solver = om.ScipyKrylov()

top.model.nonlinear_solver.linesearch = om.ArmijoGoldsteinLS()

top.setup()
top.set_val('x', np.array([2., 2, 2]).reshape(3, 1))
# Test lower bounds: should go to the lower bound and stall
top.set_val('comp.y', 0.)
top.set_val('comp.z', 1.6)
top.run_model()

for ind in range(3):
    print(top.get_val('comp.z', indices=ind))

NL: NewtonSolver 'NL: Newton' on system '' failed to converge in 10 iterations.
[1.5]
[1.5]
[1.5]

ArmijoGoldsteinLS Options#

Option	Default	Acceptable Values	Acceptable Types	Description
alpha	1.0	N/A	N/A	Initial line search step.
atol	1e-10	N/A	N/A	absolute error tolerance
bound_enforcement	scalar	['vector', 'scalar', 'wall']	N/A	If this is set to 'vector', the entire vector is backtracked together when a bound is violated. If this is set to 'scalar', only the violating entries are set to the bound and then the backtracking occurs on the vector as a whole. If this is set to 'wall', only the violating entries are set to the bound, and then the backtracking follows the wall - i.e., the violating entries do not change during the line search.
c	0.1	N/A	N/A	Slope parameter for line of sufficient decrease. The larger the step, the more decrease is required to terminate the line search.
debug_print	False	[True, False]	['bool']	If true, the values of input and output variables at the start of iteration are printed and written to a file after a failure to converge.
err_on_non_converge	False	[True, False]	['bool']	When True, AnalysisError will be raised if we don't converge.
iprint	1	N/A	['int']	whether to print output
maxiter	5	N/A	['int']	maximum number of iterations
method	Armijo	['Armijo', 'Goldstein']	N/A	Method to calculate stopping condition.
print_bound_enforce	False	N/A	N/A	Set to True to print out names and values of variables that are pulled back to their bounds.
restart_from_successful	False	[True, False]	['bool']	If True, the states are cached after a successful solve and used to restart the solver in the case of a failed solve.
retry_on_analysis_error	True	N/A	N/A	Backtrack and retry if an AnalysisError is raised.
rho	0.5	N/A	N/A	Contraction factor.
rtol	1e-10	N/A	N/A	relative error tolerance
stall_limit	0	N/A	N/A	Number of iterations after which, if the residual norms are identical within the stall_tol, then terminate as if max iterations were reached. Default is 0, which disables this feature.
stall_tol	1e-12	N/A	N/A	When stall checking is enabled, the threshold below which the residual norm is considered unchanged.
stall_tol_type	rel	['abs', 'rel']	N/A	Specifies whether the absolute or relative norm of the residual is used for stall detection.

ArmijoGoldsteinLS Constructor#

The call signature for the ArmijoGoldsteinLS constructor is:

ArmijoGoldsteinLS.__init__(**kwargs)[source]

Initialize all attributes.

ArmijoGoldsteinLS Option Examples#

bound_enforcement

ArmijoGoldsteinLS includes the bound_enforcement option in its options dictionary. This option has a dual role:

Behavior of the non-bounded variables when the bounded ones are capped.
Direction of the further backtracking.

There are three different acceptable values for bounds-enforcement schemes available in this option.

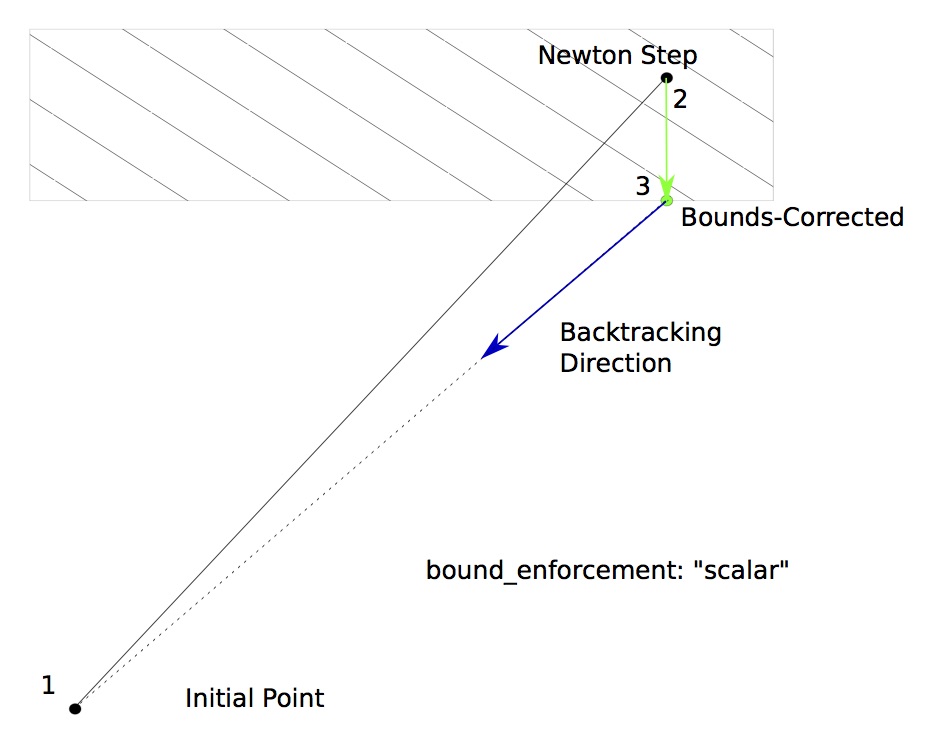
With “scalar” bounds enforcement, only the variables that violate their bounds are pulled back to feasible values; the remaining values are kept at the Newton-stepped point. This changes the direction of the backtracking vector so that it still moves in the direction of the initial point.

BT2

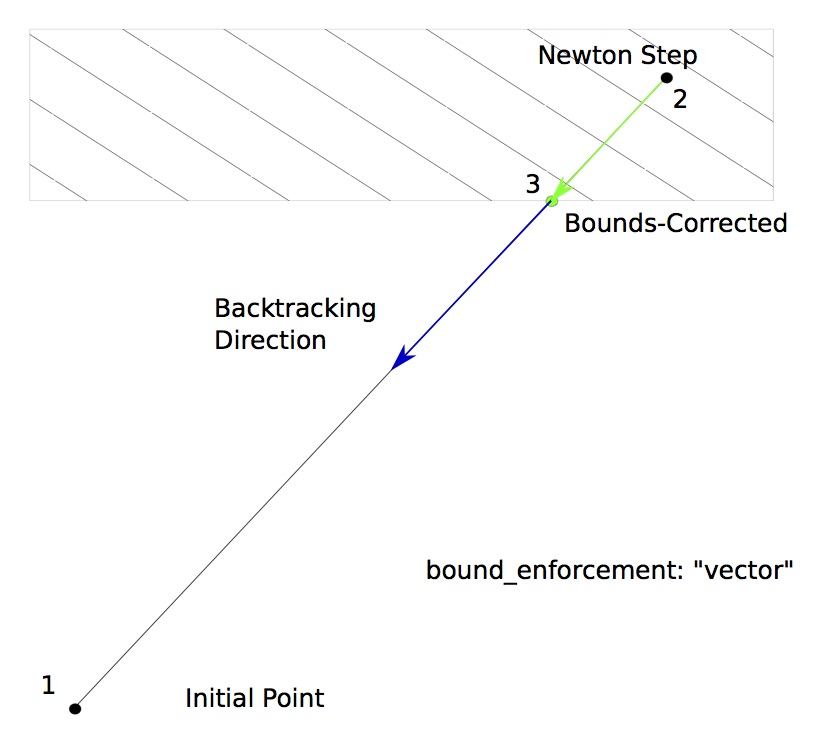
With “vector” bounds enforcement, the solution in the output vector is pulled back to a point where none of the variables violate any upper or lower bounds. Further backtracking continues along the Newton gradient direction vector back towards the initial point.

BT1

With “wall” bounds enforcement, only the variables that violate their bounds are pulled back to feasible values; the remaining values are kept at the Newton-stepped point. Further backtracking only occurs in the direction of the non-violating variables, so that it will move along the wall.

BT3

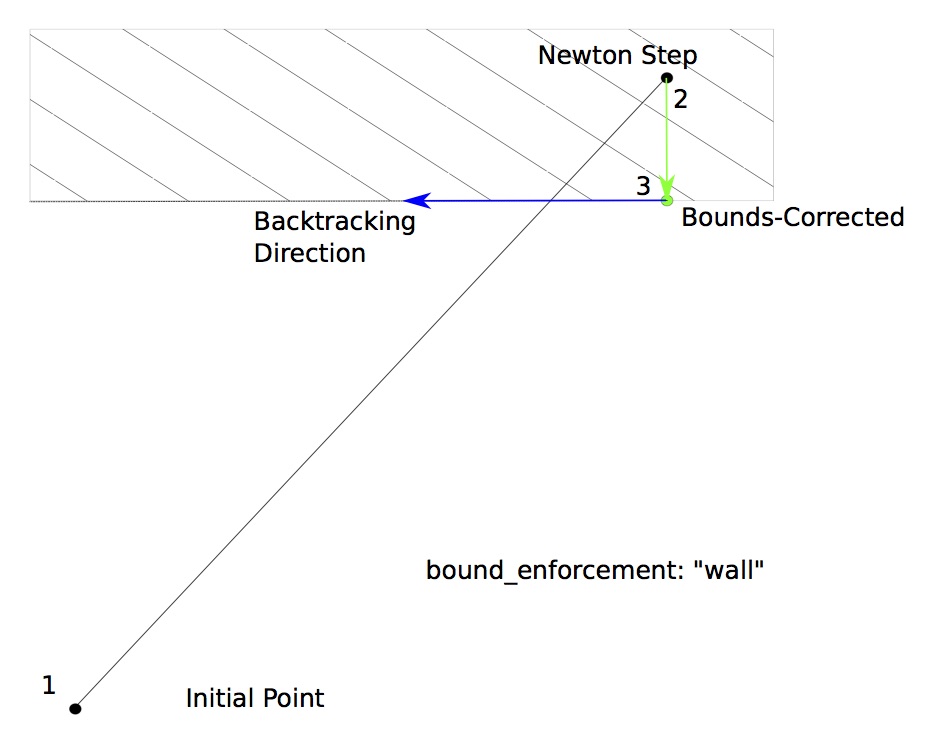
Here are examples of each acceptable value for the bound_enforcement option:

bound_enforcement: vector

The bound_enforcement option in the options dictionary is used to specify how the output bounds are enforced. When this is set to “vector”, the output vector is rolled back along the computed gradient until it reaches a point where the earliest bound violation occurred. The backtracking continues along the original computed gradient.

from openmdao.test_suite.components.implicit_newton_linesearch import ImplCompTwoStatesArrays

top = om.Problem()
top.model.add_subsystem('comp', ImplCompTwoStatesArrays(), promotes_inputs=['x'])

top.model.nonlinear_solver = om.NewtonSolver(solve_subsystems=False)
top.model.nonlinear_solver.options['maxiter'] = 10
top.model.linear_solver = om.ScipyKrylov()

top.model.nonlinear_solver.linesearch = om.ArmijoGoldsteinLS(bound_enforcement='vector')

top.setup()

top.set_val('x', np.array([2., 2, 2]).reshape(3, 1))

# Test lower bounds: should go to the lower bound and stall
top.set_val('comp.y', 0.)
top.set_val('comp.z', 1.6)
top.run_model()

for ind in range(3):
    print(top.get_val('comp.z', indices=ind))

NL: NewtonSolver 'NL: Newton' on system '' failed to converge in 10 iterations.
[1.5]
[1.5]
[1.5]

bound_enforcement: scalar

The bound_enforcement option in the options dictionary is used to specify how the output bounds are enforced. When this is set to “scaler”, then the only indices in the output vector that are rolled back are the ones that violate their upper or lower bounds. The backtracking continues along the modified gradient.

from openmdao.test_suite.components.implicit_newton_linesearch import ImplCompTwoStatesArrays

top = om.Problem()
top.model.add_subsystem('comp', ImplCompTwoStatesArrays(), promotes_inputs=['x'])

top.model.nonlinear_solver = om.NewtonSolver(solve_subsystems=False)
top.model.nonlinear_solver.options['maxiter'] = 10
top.model.linear_solver = om.ScipyKrylov()

ls = top.model.nonlinear_solver.linesearch = om.ArmijoGoldsteinLS(bound_enforcement='scalar')

top.setup()
top.set_val('x', np.array([2., 2, 2]).reshape(3, 1))
top.run_model()

NL: NewtonSolver 'NL: Newton' on system '' failed to converge in 10 iterations.

# Test lower bounds: should stop just short of the lower bound
top.set_val('comp.y', 0.)
top.set_val('comp.z', 1.6)
top.run_model()

NL: NewtonSolver 'NL: Newton' on system '' failed to converge in 10 iterations.

bound_enforcement: wall

The bound_enforcement option in the options dictionary is used to specify how the output bounds are enforced. When this is set to “wall”, then the only indices in the output vector that are rolled back are the ones that violate their upper or lower bounds. The backtracking continues along a modified gradient direction that follows the boundary of the violated output bounds.

from openmdao.test_suite.components.implicit_newton_linesearch import ImplCompTwoStatesArrays

top = om.Problem()
top.model.add_subsystem('comp', ImplCompTwoStatesArrays(), promotes_inputs=['x'])

top.model.nonlinear_solver = om.NewtonSolver(solve_subsystems=False)
top.model.nonlinear_solver.options['maxiter'] = 10
top.model.linear_solver = om.ScipyKrylov()

top.model.nonlinear_solver.linesearch = om.ArmijoGoldsteinLS(bound_enforcement='wall')

top.setup()

top.set_val('x', np.array([0.5, 0.5, 0.5]).reshape(3, 1))

# Test upper bounds: should go to the upper bound and stall
top.set_val('comp.y', 0.)
top.set_val('comp.z', 2.4)
top.run_model()

print(top.get_val('comp.z', indices=0))
print(top.get_val('comp.z', indices=1))
print(top.get_val('comp.z', indices=2))

NL: NewtonSolver 'NL: Newton' on system '' failed to converge in 10 iterations.
[2.6]
[2.5]
[2.65]

maxiter

The “maxiter” option is a termination criteria that specifies the maximum number of backtracking steps to allow.

alpha

The “alpha” option is used to specify the initial length of the Newton step. Since NewtonSolver assumes a step size of 1.0, this value usually shouldn’t be changed.

rho

The “rho” option controls how far to backtrack in each successive backtracking step. It is applied as a multiplier to the step, so a higher value (approaching 1.0) is a very small step, while a low value takes you close to the initial point. The default value is 0.5.

c

In the ArmijoGoldsteinLS, the “c” option is a multiplier on the slope check. Setting it to a smaller value means a more gentle slope will satisfy the condition and terminate.

print_bound_enforce

When the “print_bound_enforce” option is set to True, the line-search will print the name and values of any variables that exceeded their lower or upper bounds and were drawn back during bounds enforcement.

from openmdao.test_suite.components.implicit_newton_linesearch import ImplCompTwoStatesArrays

top = om.Problem()
top.model.add_subsystem('comp', ImplCompTwoStatesArrays(), promotes_inputs=['x'])

newt = top.model.nonlinear_solver = om.NewtonSolver(solve_subsystems=False)
top.model.nonlinear_solver.options['maxiter'] = 2
top.model.linear_solver = om.ScipyKrylov()

ls = newt.linesearch = om.BoundsEnforceLS(bound_enforcement='vector')
ls.options['print_bound_enforce'] = True

top.set_solver_print(level=2)


top.setup()
top.set_val('x', np.array([2., 2, 2]).reshape(3, 1))

# Test lower bounds: should go to the lower bound and stall
top.set_val('comp.y', 0.)
top.set_val('comp.z', 1.6)
top.run_model()

for ind in range(3):
    print(top.get_val('comp.z', indices=ind))

NL: Newton 0 ; 9.1126286 1
|  LN: SCIPY 0 ; 0.18556153 1
|  LN: SCIPY 1 ; 5.89504879e-16 3.17687012e-15
|  LS: BCHK 0 ; 5.69539287 0.625
NL: Newton 1 ; 5.69539287 0.625
|  LN: SCIPY 0 ; 0.0742246119 1
|  LN: SCIPY 1 ; 4.04947533e-17 5.45570428e-16
|  LS: BCHK 0 ; 5.69539287 1
NL: Newton 2 ; 5.69539287 0.625
NL: NewtonSolver 'NL: Newton' on system '' failed to converge in 2 iterations.
[1.5]
[1.5]
[1.5]

/usr/share/miniconda/envs/test/lib/python3.11/site-packages/openmdao/solvers/linesearch/backtracking.py:39: SolverWarning:'comp.z' exceeds lower bounds
  Val: [1.33333333 1.33333333 1.33333333]
  Lower: [1.5 1.5 1.5]

/usr/share/miniconda/envs/test/lib/python3.11/site-packages/openmdao/solvers/linesearch/backtracking.py:39: SolverWarning:'comp.z' exceeds lower bounds
  Val: [1.33333333 1.33333333 1.33333333]
  Lower: [1.5 1.5 1.5]

retry_on_analysis_error

By default, the ArmijoGoldsteinLS linesearch will backtrack if the model raises an AnalysisError, which can happen if the component explicitly raises it, or a subsolver hits its iteration limit with the ‘err_on_non_converge’ option set to True. If you would rather terminate on an AnalysisError, you can set this option to False.

ArmijoGoldsteinLS

Contents

ArmijoGoldsteinLS#

ArmijoGoldsteinLS Options#

ArmijoGoldsteinLS Constructor#

ArmijoGoldsteinLS Option Examples#