Providing an Initial Guess for Implicit States in a Group

In the documentation for ImplicitComponent, you saw that you can provide an initial guess for implicit states within the component using it’s guess_nonlinear method.

Group also provides a guess_nonlinear method in which you can supply the starting value for implicit state variables in any of it’s subsystems.

The following example demonstrates the capability of setting the initial guess value at the group level, using the input from one component to compute the guess for another. In this case, a Discipline group solves a system of equations using a BalanceComp. It answers the question: “What is \(x\) such that \(x^2\) is equal to twice our input value”.

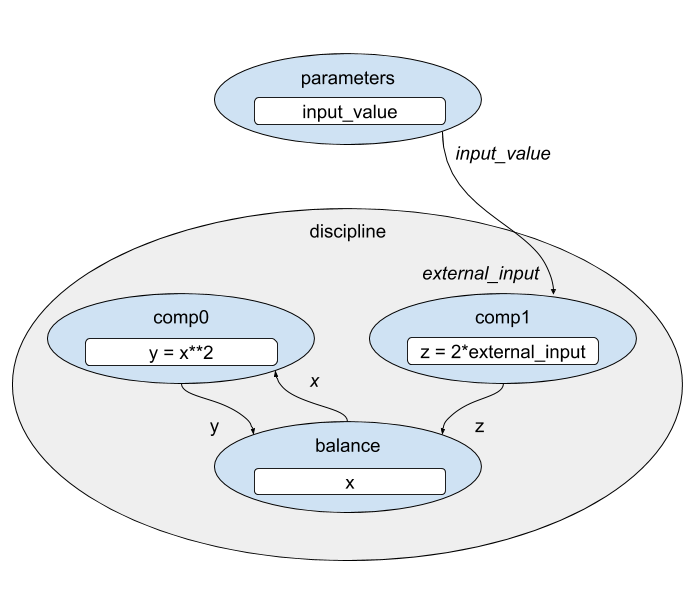
Given our knowledge of the relationship between the two equations, we can supply an initial guess for the implicit state variable, \(x\), that makes it unnecessary for the solver to iterate.

In guess_nonlinear we explicitly run the run_apply_nonlinear method to make sure the residual values are in sync with the input values.

In this case we test all of the residual values. If we tested only the residual of 'x', it would be exactly zero on the first iteration based on the way the BalanceComp computes its residuals and the initial values of the inputs. Testing all of the residuals provides a better check to see if the system is nearly converged.

This model contains two copies of the same Discipline Group. One of these groups provides a guess_nonlinear method, while the other one does not.

The following example prints the iteration history of the nonlinear solver to demonstrate how using guess_nonlinear can reduce the number of iterations required.

import numpy as np
import openmdao.api as om


class Discipline(om.Group):

    def setup(self):
        self.add_subsystem('comp0', om.ExecComp('y=x**2'))
        self.add_subsystem('comp1', om.ExecComp('z=2*external_input'),
                           promotes_inputs=['external_input'])

        self.add_subsystem('balance', om.BalanceComp('x', lhs_name='y', rhs_name='z'),
                           promotes_outputs=['x'])

        self.connect('comp0.y', 'balance.y')
        self.connect('comp1.z', 'balance.z')

        self.connect('x', 'comp0.x')

        self.nonlinear_solver = om.NewtonSolver(iprint=2, solve_subsystems=True)
        self.linear_solver = om.DirectSolver()

    def guess_nonlinear(self, inputs, outputs, residuals):
        # Update the residuals based on the inputs
        self.run_apply_nonlinear()
        
        # Check residuals so that we don't reset x if we're nearly converged.
        if np.any(np.abs(residuals.asarray()) > 1.0E-2):
            # inputs are addressed using full path name, regardless of promotion
            external_input = inputs['comp1.external_input']

            # balance drives x**2 = 2*external_input
            x_guess = (2*external_input)**.5

            # outputs are addressed by the their promoted names
            outputs['x'] = x_guess # perfect guess should converge in 0 iterations


class DisciplineNoGuess(Discipline):
    
    def guess_nonlinear(self, inputs, outputs, residuals):
        pass
            

p = om.Problem()

p.model.add_subsystem('discipline', Discipline(), promotes_inputs=['external_input'])
p.model.add_subsystem('discipline_no_guess', DisciplineNoGuess(), promotes_inputs=['external_input'])

p.setup()

p.set_val('external_input', 1.1)

p.run_model()


print('\nchanging external input to a different value and rerunning the model')
p.set_val('external_input', 1.0)

p.run_model()

print()
print(f"x_with_guess = {p.get_val('discipline.x')}")
print(f"x_no_guess = {p.get_val('discipline_no_guess.x')}")

==========
discipline
==========
NL: Newton 0 ; 0 0
NL: Newton Converged

===================
discipline_no_guess
===================
NL: Newton 0 ; 0.545454545 1
NL: Newton 1 ; 0.163636364 0.3
NL: Newton 2 ; 0.00575284091 0.010546875
NL: Newton 3 ; 8.22646906e-06 1.50818599e-05
NL: Newton 4 ; 1.69187896e-11 3.10177809e-11
NL: Newton Converged

changing external input to a different value and rerunning the model

==========
discipline
==========
NL: Newton 0 ; 2.22044605e-16 1
NL: Newton Converged

===================
discipline_no_guess
===================
NL: Newton 0 ; 0.1 1
NL: Newton 1 ; 0.00227272727 0.0227272727
NL: Newton 2 ; 1.28839415e-06 1.28839415e-05
NL: Newton 3 ; 4.15001367e-13 4.15001367e-12
NL: Newton Converged

x_with_guess = [1.41421356]
x_no_guess = [1.41421356]

Note

When a solver is restarted from the last successful solve due to having the restart_from_sucessful option set to True, the guess_nonlinear function will not be called.