The Van der Pol Oscillator

The Van der Pol Oscillator#

In dynamics, the Van Der Pol oscillator [Wikipediacontributors20] is a non-conservative oscillator with non-linear damping. It evolves in time according to the second-order differential equation:

(16)#\[\begin{align} \frac{d^2x}{dt^2} - u (1 - x^2) \frac{dx}{dt} + x &= 0 \end{align}\]

where \(x\) is the position coordinate (a function of the time \(t\)), and \(u\) is a scalar parameter indicating the nonlinearity and the strength of the damping.

To make this an optimal control problem, we want to find the smallest control that will dampen the oscillation (drive the state variables to zero). We can express this as an objective function \(J\) to minimize:

(17)#\[\begin{align} J &= \int x^2_0 + x^2_1 + u^2 \end{align}\]

In other words, we want to find the optimal (smallest) trajectory of the control \(u\) such that the oscillation and the oscillation’s rate of change are driven to zero.

State Variables#

There are three state variables are used to define the configuration of the system at any given instant in time.

\(x_1\): The primary output of the oscillator.
\(x_0\): The rate of change of the primary output.
\(J\): The objective function to be minimized.

The objective function is included as a state variable so that Dymos will do the integration.

The \(x_1\) and \(x_0\) state variables are also inputs to the system, along with the control \(u\).

System Dynamics#

The evolution of the state variables is given by the following ordinary differential equations (ODE):

(18)#\[\begin{align} \frac{dx_0}{dt} &= (1 - x^2_1) x_0 - x_1 + u \\ \frac{dx_1}{dt} &= x_0 \\ \frac{dJ}{dt} &= x^2_0 + x^2_1 + u^2 \end{align}\]

Control Variables#

This system has a single control variable:

\(u\): The control input.

The control variable has a constraint: \(-0.75 \leq u \leq 1.0\)

The initial and final conditions#

The initial conditions are:

(19)#\[\begin{align} t_i &= 0 \\ x_{0i} &= 1 \\ x_{1i} &= 1 \\ u_i &= -0.75 \end{align}\]

The final conditions are:

(20)#\[\begin{align} t_f &= 10 \\ x_{0f} &= 0 \\ x_{1f} &= 0 \\ u_f &= 0 \end{align}\]

Defining the ODE as an OpenMDAO System#

In Dymos, the ODE is an OpenMDAO System (a Component, or a Group of components). The following ExplicitComponent computes the state rates for the Van der Pol problem.

More detail on the workings of an ExplicitComponent can be found in the OpenMDAO documentation. In summary:

initialize: Called at setup, and used to define options for the component. ALL Dymos ODE components should have the property num_nodes, which defines the number of points at which the outputs are simultaneously computed.
setup: Used to add inputs and outputs to the component, and declare which outputs (and indices of outputs) are dependent on each of the inputs.
compute: Used to compute the outputs, given the inputs.
compute_partials: Used to compute the derivatives of the outputs with respect to each of the inputs analytically. This method may be omitted if finite difference or complex-step approximations are used, though analytic is recommended.

Note

Things to note about the Van der Pol ODE system

Only the vanderpol_ode class below is important for defining the basic problem. The other classes are used to demonstrate Message Passing Interface (MPI) parallel calculation of the system. They can be ignored.
\(x_1\), \(x_0\), and \(u\) are inputs.
\(\dot{x_1}\), \(\dot{x_0}\), and \(\dot{J}\) are outputs.
declare_partials is called for every output with respect to every input.
For efficiency, partial derrivatives that are constant have values specified in the setup method rather than the compute_partials method. So although 7 partials are declared, only 5 are computed in compute_partials.
This ODE includes some additional complexity to allow it to run in parallel. See the Van der Pol example in the dymos examples directory for an example of how to run the problem under MPI.

import numpy as np
import openmdao.api as om
from openmdao.utils.array_utils import evenly_distrib_idxs


class VanderpolODE(om.ExplicitComponent):
    """intentionally slow version of vanderpol_ode for effects of demonstrating distributed component calculations

    MPI can run this component in multiple processes, distributing the calculation of derivatives.
    This code has a delay in it to simulate a longer computation. It should run faster with more processes.
    """

    def __init__(self, *args, **kwargs):
        self.progress_prints = False
        super().__init__(*args, **kwargs)

    def initialize(self):
        self.options.declare('num_nodes', types=int)
        self.options.declare('distrib', types=bool, default=False)

    def setup(self):
        nn = self.options['num_nodes']
        comm = self.comm
        rank = comm.rank

        sizes, offsets = evenly_distrib_idxs(comm.size, nn)  # (#cpus, #inputs) -> (size array, offset array)
        self.start_idx = offsets[rank]
        self.io_size = sizes[rank]  # number of inputs and outputs managed by this distributed process
        self.end_idx = self.start_idx + self.io_size

        # inputs: 2 states and a control
        self.add_input('x0', val=np.ones(nn), desc='derivative of Output', units='V/s')
        self.add_input('x1', val=np.ones(nn), desc='Output', units='V')
        self.add_input('u', val=np.ones(nn), desc='control', units=None)

        # outputs: derivative of states
        # the objective function will be treated as a state for computation, so its derivative is an output
        self.add_output('x0dot', val=np.ones(self.io_size), desc='second derivative of Output',
                        units='V/s**2', distributed=self.options['distrib'])
        self.add_output('x1dot', val=np.ones(self.io_size), desc='derivative of Output',
                        units='V/s', distributed=self.options['distrib'])
        self.add_output('Jdot', val=np.ones(self.io_size), desc='derivative of objective',
                        units='1.0/s', distributed=self.options['distrib'])

        # self.declare_coloring(method='cs')
        # # partials
        r = np.arange(self.io_size, dtype=int)
        c = r + self.start_idx

        self.declare_partials(of='x0dot', wrt='x0',  rows=r, cols=c)
        self.declare_partials(of='x0dot', wrt='x1',  rows=r, cols=c)
        self.declare_partials(of='x0dot', wrt='u',   rows=r, cols=c, val=1.0)

        self.declare_partials(of='x1dot', wrt='x0',  rows=r, cols=c, val=1.0)

        self.declare_partials(of='Jdot', wrt='x0',  rows=r, cols=c)
        self.declare_partials(of='Jdot', wrt='x1',  rows=r, cols=c)
        self.declare_partials(of='Jdot', wrt='u',   rows=r, cols=c)

    def compute(self, inputs, outputs):

        # The inputs contain the entire vector, be each rank will only operate on a portion of it.
        x0 = inputs['x0'][self.start_idx:self.end_idx]
        x1 = inputs['x1'][self.start_idx:self.end_idx]
        u = inputs['u'][self.start_idx:self.end_idx]

        outputs['x0dot'] = (1.0 - x1**2) * x0 - x1 + u
        outputs['x1dot'] = x0
        outputs['Jdot'] = x0**2 + x1**2 + u**2

    def compute_partials(self, inputs, jacobian):
        x0 = inputs['x0'][self.start_idx:self.end_idx]
        x1 = inputs['x1'][self.start_idx:self.end_idx]
        u = inputs['u'][self.start_idx:self.end_idx]

        jacobian['x0dot', 'x0'] = 1.0 - x1 * x1
        jacobian['x0dot', 'x1'] = -2.0 * x1 * x0 - 1.0

        jacobian['Jdot', 'x0'] = 2.0 * x0
        jacobian['Jdot', 'x1'] = 2.0 * x1
        jacobian['Jdot', 'u'] = 2.0 * u

Defining the Dymos Problem#

Once the ODEs are defined, they are used to create a Dymos Problem object that allows solution.

Note

Things to note about the Van der Pol Dymos Problem definition

The vanderpol function creates and returns a Dymos Problem instance that can be used for simulation or optimization.
The vanderpol function has optional arguments for specifying options for the type of transcription, number of segments, optimizer, etc. These can be ignored when first trying to understand the code.
The Problem object has a Trajectory object, and the trajectory has a single Phase. Most of the problem setup is performed by calling methods on the phase (set_time_options, add_state, add_boundary_constraint, add_objective).
The add_state and add_control calls include the target parameter for \(x_0\), \(x_1\), and \(u\). This is required so that the inputs are correctly calculated.
Initial (linear) guesses are supplied for the states and control.

import openmdao.api as om
import dymos as dm

def vanderpol(transcription='gauss-lobatto', num_segments=15, transcription_order=3,
              compressed=True, optimizer='SLSQP', use_pyoptsparse=False):
    """Dymos problem definition for optimal control of a Van der Pol oscillator"""

    # define the OpenMDAO problem
    p = om.Problem(model=om.Group())

    if not use_pyoptsparse:
        p.driver = om.ScipyOptimizeDriver()
    else:
        p.driver = om.pyOptSparseDriver(print_results=False)
    p.driver.options['optimizer'] = optimizer
    if use_pyoptsparse:
        if optimizer == 'SNOPT':
            p.driver.opt_settings['iSumm'] = 6  # show detailed SNOPT output
        elif optimizer == 'IPOPT':
            p.driver.opt_settings['print_level'] = 4
    p.driver.declare_coloring()

    # define a Trajectory object and add to model
    traj = dm.Trajectory()
    p.model.add_subsystem('traj', subsys=traj)

    # define a Transcription
    if transcription == 'gauss-lobatto':
        t = dm.GaussLobatto(num_segments=num_segments,
                            order=transcription_order,
                            compressed=compressed)
    elif transcription == 'radau-ps':
        t = dm.Radau(num_segments=num_segments,
                     order=transcription_order,
                     compressed=compressed)

    # define a Phase as specified above and add to Phase
    phase = dm.Phase(ode_class=VanderpolODE, transcription=t)
    traj.add_phase(name='phase0', phase=phase)

    t_final = 10
    phase.set_time_options(fix_initial=True, fix_duration=True, duration_val=t_final, units='s')

    # set the State time options
    phase.add_state('x0', fix_initial=True, fix_final=True,
                    rate_source='x0dot',
                    units='V/s', ref=0.1, defect_ref=0.1)  # target required because x0 is an input
    phase.add_state('x1', fix_initial=True, fix_final=True,
                    rate_source='x1dot',
                    units='V', ref=0.1, defect_ref=0.1)
    phase.add_state('J', fix_initial=True, fix_final=False,
                    rate_source='Jdot',
                    units=None)

    # define the control
    phase.add_control(name='u', units=None, lower=-0.75, upper=1.0, continuity=True,
                      rate_continuity=True)

    # define objective to minimize
    phase.add_objective('J', loc='final')

    # setup the problem
    p.setup(check=True)

    phase.set_time_val(0.0, t_final)

    # add a linearly interpolated initial guess for the state and control curves
    phase.set_state_val('x0', [1, 0])
    phase.set_state_val('x0', [1, 0])
    phase.set_state_val('x0', [0, 1])
    phase.set_control_val('u', -0.75)

    return p

Simulating the Problem (without control)#

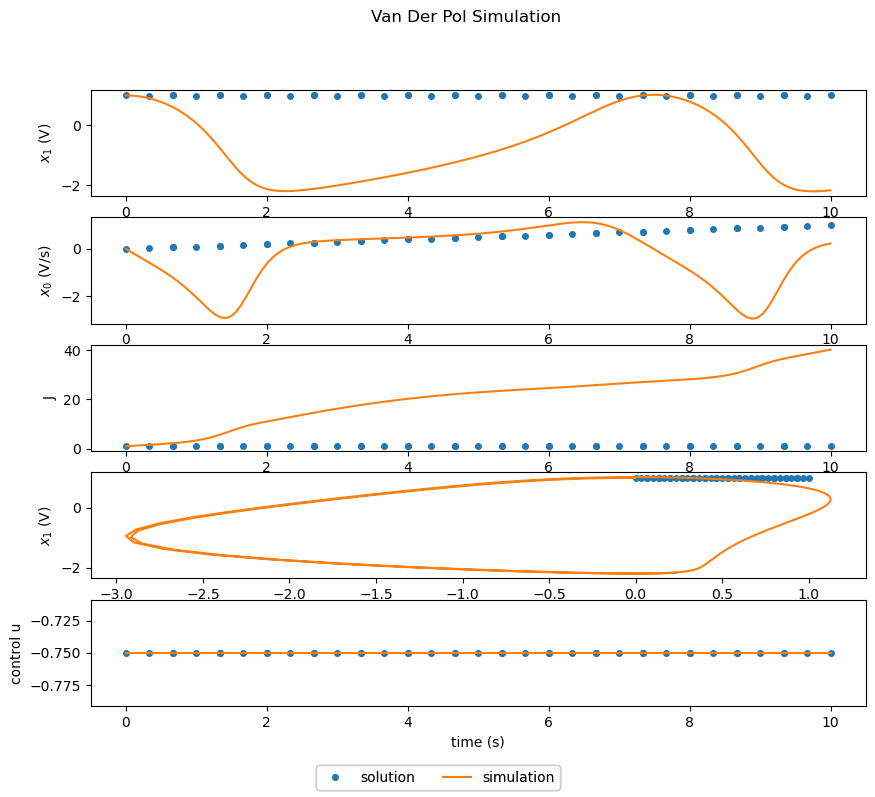
The following script creates an instance of the Dymos vanderpol problem and simulates it.

Since the problem was only simulated and not solved, the solution lines in the plots show only the initial guesses for \(x_0\), \(x_1\), and \(u\). The simulation lines shown in the plots are the system response with the control variable \(u\) held constant.

# Create the Dymos problem instance
p = vanderpol(transcription='gauss-lobatto', use_pyoptsparse=True, optimizer='IPOPT', num_segments=15)

# Run the problem (simulate only)
dm.run_problem(p, run_driver=False, simulate=True)

--- Constraint Report [traj] ---
    --- phase0 ---
        None

INFO: checking out_of_order

INFO: checking system

INFO: checking solvers

INFO: checking dup_inputs

INFO: checking missing_recorders

INFO: checking unserializable_options

INFO: checking comp_has_no_outputs

INFO: checking auto_ivc_warnings

Model viewer data has already been recorded for Driver.
INFO: checking out_of_order

INFO: checking system

INFO: checking solvers

INFO: checking dup_inputs

INFO: checking missing_recorders

INFO: checking unserializable_options

INFO: checking comp_has_no_outputs

INFO: checking auto_ivc_warnings

/usr/share/miniconda/envs/test/lib/python3.11/site-packages/openmdao/core/group.py:1137: DerivativesWarning:Constraints or objectives [ode_eval.control_interp.control_rates:u_rate, ode_eval.control_interp.control_rates:u_rate2, ode_eval.control_interp.control_values:u] cannot be impacted by the design variables of the problem because no partials were defined for them in their parent component(s).

Simulating trajectory traj
Model viewer data has already been recorded for Driver.

Done simulating trajectory traj

The first two plots shows the variables \(x_0\) and \(x_1\) vs time. The third plots shows \(x_0\) vs. \(x_1\) (which will be mostly circular in the case of undamped oscillation). The final plot is the (fixed) control variable \(u\) vs time.

(<Figure size 1000x800 with 5 Axes>,
 array([<Axes: xlabel='time (s)', ylabel='$x_1$ (V)'>,
        <Axes: xlabel='time (s)', ylabel='$x_0$ (V/s)'>,
        <Axes: xlabel='time (s)', ylabel='J'>,
        <Axes: xlabel='$x_0$ (V/s)', ylabel='$x_1$ (V)'>,
        <Axes: xlabel='time (s)', ylabel='control u'>], dtype=object))

../../_images/727fcc94e4e9321b82e701d4824ab4e4f2dd642a442ae2efd34033454544d6ef.png

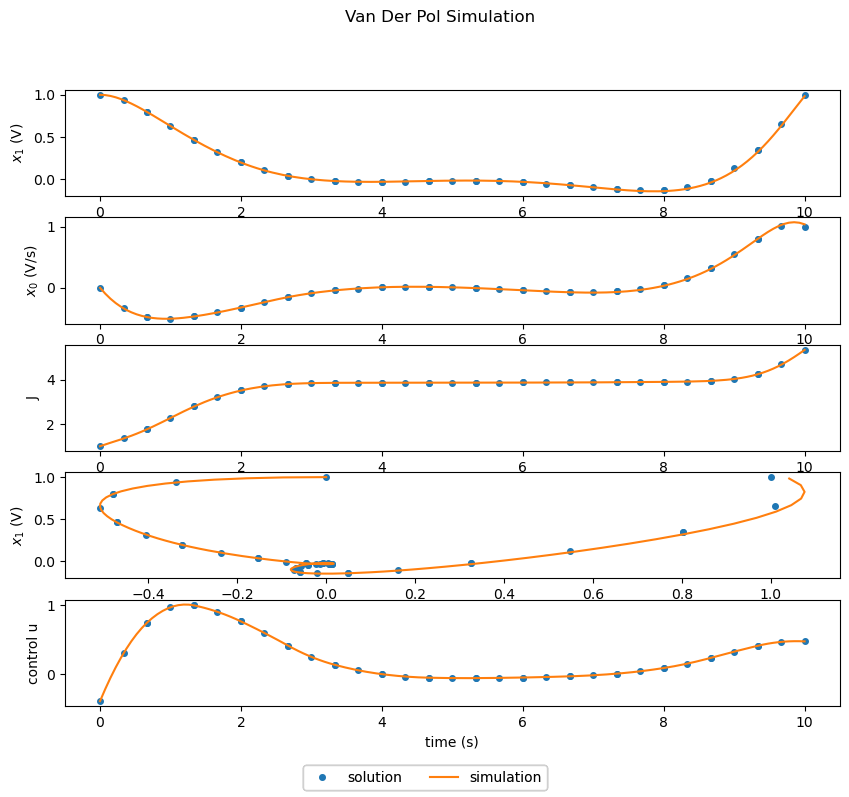
Solving the Optimal Control Problem#

The next example shows optimization followed by simulation.

With a successful optimization, the resulting plots show a good match between the simulated (with varying control) and optimized results. The state variables \(x_0\) and \(x_1\) as well as the control variable \(u\) are all driven to zero.

However one can notice that the distribution of segments/nodes in the phase results in a bit of error. If we take the simulation results as the truth, there is a bit of divergence in the state values of the solution and simulation towards the end.

import dymos as dm

# Create the Dymos problem instance
p = vanderpol(transcription='gauss-lobatto', num_segments=15,
              transcription_order=3, compressed=False, use_pyoptsparse=True, optimizer='IPOPT')

# Find optimal control solution to stop oscillation
dm.run_problem(p, simulate=True)

--- Constraint Report [traj] ---
    --- phase0 ---
        None

INFO: checking out_of_order

INFO: checking system

INFO: checking solvers

INFO: checking dup_inputs

INFO: checking missing_recorders

INFO: checking unserializable_options

INFO: checking comp_has_no_outputs

INFO: checking auto_ivc_warnings

Model viewer data has already been recorded for Driver.
INFO: checking out_of_order

INFO: checking system

INFO: checking solvers

INFO: checking dup_inputs

INFO: checking missing_recorders

INFO: checking unserializable_options

INFO: checking comp_has_no_outputs

INFO: checking auto_ivc_warnings

Full total jacobian for problem 'problem4' was computed 3 times, taking 0.0982814110000163 seconds.
Total jacobian shape: (60, 130) 


Jacobian shape: (60, 130)  (5.15% nonzero)
FWD solves: 0   REV solves: 5
Total colors vs. total size: 5 vs 60  (91.67% improvement)

Sparsity computed using tolerance: 1e-25
Time to compute sparsity:   0.0983 sec
Time to compute coloring:   0.0329 sec
Memory to compute coloring:   0.2500 MB
Coloring created on: 2024-11-18 20:35:24

List of user-set options:

                                    Name   Value                used
                        file_print_level = 5                     yes
                   hessian_approximation = limited-memory        yes
                           linear_solver = mumps                 yes
                      nlp_scaling_method = user-scaling          yes
                             output_file = /home/runner/work/dymos/dymos/docs/dymos_book/examples/vanderpol/problem4_out/IPOPT.out  yes
                             print_level = 4                     yes
                      print_user_options = yes                   yes
                                      sb = yes                   yes

Total number of variables............................:      130
                     variables with only lower bounds:        0
                variables with lower and upper bounds:       45
                     variables with only upper bounds:        0
Total number of equality constraints.................:      115
Total number of inequality constraints...............:        0
        inequality constraints with only lower bounds:        0
   inequality constraints with lower and upper bounds:        0
        inequality constraints with only upper bounds:        0

Number of Iterations....: 31

                                   (scaled)                 (unscaled)
Objective...............:   5.3660057662482838e+00    5.3660057662482838e+00
Dual infeasibility......:   5.6637226194345783e-09    5.6637226194345783e-09
Constraint violation....:   5.9674487573602164e-15    5.9674487573602164e-15
Variable bound violation:   9.8138401849467982e-09    9.8138401849467982e-09
Complementarity.........:   1.0000001538242471e-11    1.0000001538242471e-11
Overall NLP error.......:   5.6637226194345783e-09    5.6637226194345783e-09


Number of objective function evaluations             = 33
Number of objective gradient evaluations             = 32
Number of equality constraint evaluations            = 33
Number of inequality constraint evaluations          = 0
Number of equality constraint Jacobian evaluations   = 32
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations             = 0
Total seconds in IPOPT                               = 0.696

EXIT: Optimal Solution Found.

/usr/share/miniconda/envs/test/lib/python3.11/site-packages/openmdao/visualization/opt_report/opt_report.py:625: UserWarning: Attempting to set identical low and high ylims makes transformation singular; automatically expanding.
  ax.set_ylim([ymin_plot, ymax_plot])

/usr/share/miniconda/envs/test/lib/python3.11/site-packages/openmdao/core/group.py:1137: DerivativesWarning:Constraints or objectives [ode_eval.control_interp.control_rates:u_rate, ode_eval.control_interp.control_rates:u_rate2, ode_eval.control_interp.control_values:u] cannot be impacted by the design variables of the problem because no partials were defined for them in their parent component(s).

Simulating trajectory traj
Model viewer data has already been recorded for Driver.

Done simulating trajectory traj

Problem: problem4
Driver:  pyOptSparseDriver
  success     : True
  iterations  : 35
  runtime     : 8.6022E-01 s
  model_evals : 35
  model_time  : 2.6102E-02 s
  deriv_evals : 33
  deriv_time  : 1.1156E-01 s
  exit_status : SUCCESS

(<Figure size 1000x800 with 5 Axes>,
 array([<Axes: xlabel='time (s)', ylabel='$x_1$ (V)'>,
        <Axes: xlabel='time (s)', ylabel='$x_0$ (V/s)'>,
        <Axes: xlabel='time (s)', ylabel='J'>,
        <Axes: xlabel='$x_0$ (V/s)', ylabel='$x_1$ (V)'>,
        <Axes: xlabel='time (s)', ylabel='control u'>], dtype=object))

../../_images/bbce8ac7ddfb0e4aa2d47cee73eb8818f7bc96e4a1da74446a39e7130b8d6cb2.png

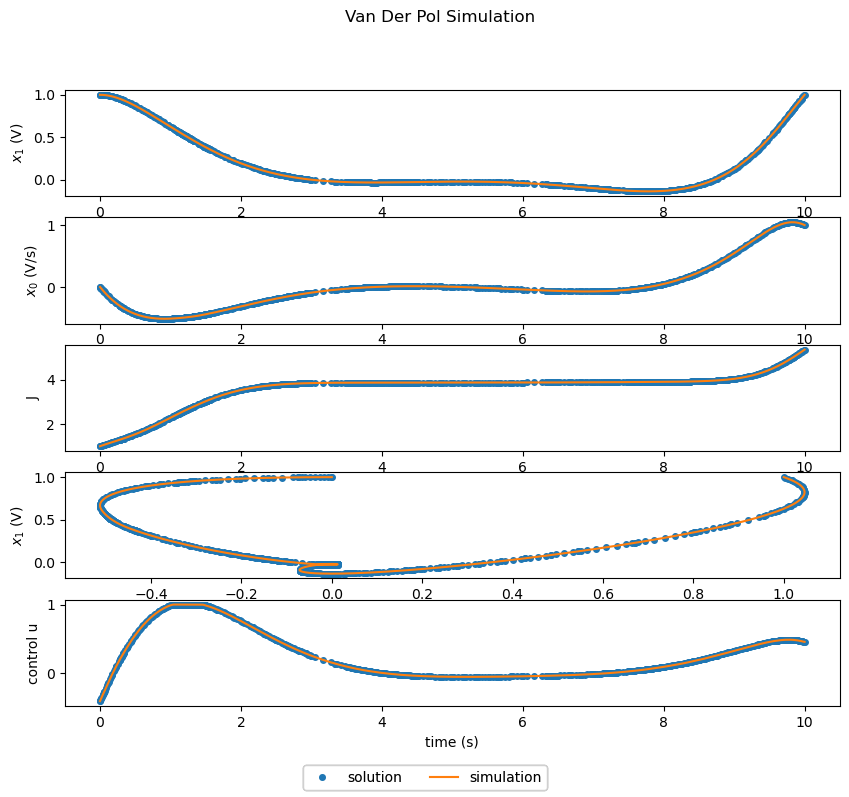
Solving the Optimal Control Problem with Grid Refinement#

Repeating the optimization with grid refinement enabled requires changing only two lines in the code. For the sake of grid refinement demonstration, the initial number of segments is also reduced by a factor of 5.

Optimization with grid refinement gets results similar to the example without grid refinement, but runs faster and does not require supplying a good guess for the number segments.

# Create the Dymos problem instance
p = vanderpol(transcription='gauss-lobatto', num_segments=15,
              transcription_order=3, compressed=True, optimizer='SLSQP')

# Enable grid refinement and find optimal control solution to stop oscillation
p.model.traj.phases.phase0.set_refine_options(refine=True, tol=1.0E-6)

dm.run_problem(p, simulate=True, refine_iteration_limit=5, refine_method='hp')

--- Constraint Report [traj] ---
    --- phase0 ---
        None

INFO: checking out_of_order

INFO: checking out_of_order

INFO: checking system

INFO: checking system

INFO: checking solvers

INFO: checking solvers

INFO: checking dup_inputs

INFO: checking dup_inputs

INFO: checking missing_recorders

INFO: checking missing_recorders

INFO: checking unserializable_options

INFO: checking unserializable_options

INFO: checking comp_has_no_outputs

INFO: checking comp_has_no_outputs

INFO: checking auto_ivc_warnings

INFO: checking auto_ivc_warnings

Model viewer data has already been recorded for Driver.
INFO: checking out_of_order

INFO: checking out_of_order

INFO: checking system

INFO: checking system

INFO: checking solvers

INFO: checking solvers

INFO: checking dup_inputs

INFO: checking dup_inputs

INFO: checking missing_recorders

INFO: checking missing_recorders

INFO: checking unserializable_options

INFO: checking unserializable_options

INFO: checking comp_has_no_outputs

INFO: checking comp_has_no_outputs

INFO: checking auto_ivc_warnings

INFO: checking auto_ivc_warnings

Full total jacobian for problem 'problem7' was computed 3 times, taking 0.09904828799994903 seconds.
Total jacobian shape: (60, 74) 


Jacobian shape: (60, 74)  (8.74% nonzero)
FWD solves: 9   REV solves: 0
Total colors vs. total size: 9 vs 74  (87.84% improvement)

Sparsity computed using tolerance: 1e-25
Time to compute sparsity:   0.0990 sec
Time to compute coloring:   0.0254 sec
Memory to compute coloring:   0.0000 MB
Coloring created on: 2024-11-18 20:35:26

Optimization terminated successfully    (Exit mode 0)
            Current function value: 5.3660108149594405
            Iterations: 43
            Function evaluations: 45
            Gradient evaluations: 43
Optimization Complete
-----------------------------------

==================================================
          Grid Refinement - Iteration 1           
--------------------------------------------------
    Phase: traj.phases.phase0
        Refinement Options:
            Allow Refinement = True
            Tolerance = 1e-06
            Min Order = 3
            Max Order = 14
        Original Grid:
            Number of Segments = 15
            Segment Ends = [-1.0, -0.8667, -0.7333, -0.6, -0.4667, -0.3333, -0.2, -0.0667, 0.0667, 0.2, 0.3333, 0.4667, 0.6, 0.7333, 0.8667, 1.0]
            Segment Order = [3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3]
            Error = [0.006161, 0.002225, 0.0003765, 0.0006652, 0.0003891, 0.0002518, 0.0001769, 9.822e-05, 0.0001306, 0.0002293, 0.0004298, 0.0005999, 0.0009525, 0.001663, 0.005445]
    Phase: traj.phases.phase0
        New Grid:
            Number of Segments = 15
            Segment Ends = [-1.0, -0.8667, -0.7333, -0.6, -0.4667, -0.3333, -0.2, -0.0667, 0.0667, 0.2, 0.3333, 0.4667, 0.6, 0.7333, 0.8667, 1.0]
            Segment Order = [5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5]
        Refined: True


--- Constraint Report [traj] ---
    --- phase0 ---
        None

Model viewer data has already been recorded for Driver.

/usr/share/miniconda/envs/test/lib/python3.11/site-packages/openmdao/core/system.py:4357: OpenMDAOWarning:Calling `list_inputs` before `final_setup` will only display the default values of variables and will not show the result of any `set_val` calls.
/usr/share/miniconda/envs/test/lib/python3.11/site-packages/dymos/phase/phase.py:3056: OpenMDAOWarning:phase0.states:x0 specifies 'fix_final=True'. If the given restart file has a different final value this will overwrite the user-specified value
/usr/share/miniconda/envs/test/lib/python3.11/site-packages/dymos/phase/phase.py:3056: OpenMDAOWarning:phase0.states:x1 specifies 'fix_final=True'. If the given restart file has a different final value this will overwrite the user-specified value

Full total jacobian for problem 'problem7' was computed 3 times, taking 0.19049168599997301 seconds.
Total jacobian shape: (105, 149) 


Jacobian shape: (105, 149)  (6.78% nonzero)
FWD solves: 14   REV solves: 0
Total colors vs. total size: 14 vs 149  (90.60% improvement)

Sparsity computed using tolerance: 1e-25
Time to compute sparsity:   0.1905 sec
Time to compute coloring:   0.0518 sec
Memory to compute coloring:   0.0000 MB
Coloring created on: 2024-11-18 20:35:28

Optimization terminated successfully    (Exit mode 0)
            Current function value: 5.358596871051769
            Iterations: 20
            Function evaluations: 21
            Gradient evaluations: 20
Optimization Complete
-----------------------------------


==================================================
          Grid Refinement - Iteration 2           
--------------------------------------------------
    Phase: traj.phases.phase0
        Refinement Options:
            Allow Refinement = True
            Tolerance = 1e-06
            Min Order = 3
            Max Order = 14
        Original Grid:
            Number of Segments = 15
            Segment Ends = [-1.0, -0.8667, -0.7333, -0.6, -0.4667, -0.3333, -0.2, -0.0667, 0.0667, 0.2, 0.3333, 0.4667, 0.6, 0.7333, 0.8667, 1.0]
            Segment Order = [5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5]
            Error = [5.094e-05, 0.0001477, 3.45e-05, 2.844e-06, 3.926e-06, 4.835e-06, 5.746e-07, 7.534e-07, 2.641e-07, 5.137e-07, 9.828e-07, 7.437e-07, 5.633e-06, 2.418e-05, 0.0001262]
    Phase: traj.phases.phase0
        New Grid:
            Number of Segments = 24
            Segment Ends = [-1.0, -0.9333, -0.8667, -0.8, -0.7333, -0.6667, -0.6, -0.5333, -0.4667, -0.4, -0.3333, -0.2667, -0.2, -0.0667, 0.0667, 0.2, 0.3333, 0.4667, 0.6, 0.6667, 0.7333, 0.8, 0.8667, 0.9333, 1.0]
            Segment Order = [5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5]
        Refined: True


--- Constraint Report [traj] ---
    --- phase0 ---
        None

Model viewer data has already been recorded for Driver.

/usr/share/miniconda/envs/test/lib/python3.11/site-packages/openmdao/core/system.py:4357: OpenMDAOWarning:Calling `list_inputs` before `final_setup` will only display the default values of variables and will not show the result of any `set_val` calls.
/usr/share/miniconda/envs/test/lib/python3.11/site-packages/dymos/phase/phase.py:3056: OpenMDAOWarning:phase0.states:x0 specifies 'fix_final=True'. If the given restart file has a different final value this will overwrite the user-specified value
/usr/share/miniconda/envs/test/lib/python3.11/site-packages/dymos/phase/phase.py:3056: OpenMDAOWarning:phase0.states:x1 specifies 'fix_final=True'. If the given restart file has a different final value this will overwrite the user-specified value

Full total jacobian for problem 'problem7' was computed 3 times, taking 0.3179826159999948 seconds.
Total jacobian shape: (168, 239) 


Jacobian shape: (168, 239)  (4.28% nonzero)
FWD solves: 14   REV solves: 0
Total colors vs. total size: 14 vs 239  (94.14% improvement)

Sparsity computed using tolerance: 1e-25
Time to compute sparsity:   0.3180 sec
Time to compute coloring:   0.0818 sec
Memory to compute coloring:   0.0000 MB
Coloring created on: 2024-11-18 20:35:29

Optimization terminated successfully    (Exit mode 0)
            Current function value: 5.358599248000944
            Iterations: 14
            Function evaluations: 15
            Gradient evaluations: 14
Optimization Complete
-----------------------------------


==================================================
          Grid Refinement - Iteration 3           
--------------------------------------------------
    Phase: traj.phases.phase0
        Refinement Options:
            Allow Refinement = True
            Tolerance = 1e-06
            Min Order = 3
            Max Order = 14
        Original Grid:
            Number of Segments = 24
            Segment Ends = [-1.0, -0.9333, -0.8667, -0.8, -0.7333, -0.6667, -0.6, -0.5333, -0.4667, -0.4, -0.3333, -0.2667, -0.2, -0.0667, 0.0667, 0.2, 0.3333, 0.4667, 0.6, 0.6667, 0.7333, 0.8, 0.8667, 0.9333, 1.0]
            Segment Order = [5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5]
            Error = [7.218e-06, 1.469e-06, 2.139e-06, 1.588e-05, 2.289e-05, 4.472e-06, 2.876e-07, 1.038e-07, 2.457e-07, 2.424e-07, 9.594e-08, 1.292e-06, 3.48e-06, 1.496e-06, 5.182e-07, 2.443e-06, 6.638e-06, 1.256e-05, 3.437e-06, 7.518e-07, 2.351e-07, 4.981e-07, 3.252e-06, 7.969e-06]
    Phase: traj.phases.phase0
        New Grid:
            Number of Segments = 34
            Segment Ends = [-1.0, -0.9667, -0.9333, -0.8667, -0.8, -0.7667, -0.7333, -0.7, -0.6667, -0.6333, -0.6, -0.5333, -0.4667, -0.4, -0.3333, -0.2667, -0.2, -0.1333, -0.0667, 0.0667, 0.2, 0.2667, 0.3333, 0.4, 0.4667, 0.5333, 0.6, 0.6333, 0.6667, 0.7333, 0.8, 0.8667, 0.9333, 0.9667, 1.0]
            Segment Order = [5, 5, 7, 9, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 11, 5, 5, 13, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 9, 5, 5]
        Refined: True

--- Constraint Report [traj] ---
    --- phase0 ---
        None

Model viewer data has already been recorded for Driver.

/usr/share/miniconda/envs/test/lib/python3.11/site-packages/dymos/grid_refinement/hp_adaptive/hp_adaptive.py:379: RuntimeWarning: divide by zero encountered in divide
  q_smooth = (np.log(self.error[phase_path][smooth_need_refine_idxs] /
/usr/share/miniconda/envs/test/lib/python3.11/site-packages/dymos/grid_refinement/hp_adaptive/hp_adaptive.py:411: RuntimeWarning: divide by zero encountered in divide
  q_split = np.log((self.error[phase_path][split_seg_idxs] /
/usr/share/miniconda/envs/test/lib/python3.11/site-packages/openmdao/core/system.py:4357: OpenMDAOWarning:Calling `list_inputs` before `final_setup` will only display the default values of variables and will not show the result of any `set_val` calls.
/usr/share/miniconda/envs/test/lib/python3.11/site-packages/dymos/phase/phase.py:3056: OpenMDAOWarning:phase0.states:x0 specifies 'fix_final=True'. If the given restart file has a different final value this will overwrite the user-specified value
/usr/share/miniconda/envs/test/lib/python3.11/site-packages/dymos/phase/phase.py:3056: OpenMDAOWarning:phase0.states:x1 specifies 'fix_final=True'. If the given restart file has a different final value this will overwrite the user-specified value

Full total jacobian for problem 'problem7' was computed 3 times, taking 0.5780054699999937 seconds.
Total jacobian shape: (274, 399) 


Jacobian shape: (274, 399)  (3.16% nonzero)
FWD solves: 0   REV solves: 27
Total colors vs. total size: 27 vs 274  (90.15% improvement)

Sparsity computed using tolerance: 1e-25
Time to compute sparsity:   0.5780 sec
Time to compute coloring:   0.1458 sec
Memory to compute coloring:   0.0000 MB
Coloring created on: 2024-11-18 20:35:30

Optimization terminated successfully    (Exit mode 0)
            Current function value: 5.358600436411783
            Iterations: 7
            Function evaluations: 8
            Gradient evaluations: 7
Optimization Complete
-----------------------------------


==================================================
          Grid Refinement - Iteration 4           
--------------------------------------------------
    Phase: traj.phases.phase0
        Refinement Options:
            Allow Refinement = True
            Tolerance = 1e-06
            Min Order = 3
            Max Order = 14
        Original Grid:
            Number of Segments = 34
            Segment Ends = [-1.0, -0.9667, -0.9333, -0.8667, -0.8, -0.7667, -0.7333, -0.7, -0.6667, -0.6333, -0.6, -0.5333, -0.4667, -0.4, -0.3333, -0.2667, -0.2, -0.1333, -0.0667, 0.0667, 0.2, 0.2667, 0.3333, 0.4, 0.4667, 0.5333, 0.6, 0.6333, 0.6667, 0.7333, 0.8, 0.8667, 0.9333, 0.9667, 1.0]
            Segment Order = [5, 5, 7, 9, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 11, 5, 5, 13, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 9, 5, 5]
            Error = [4.532e-07, 2.332e-07, 1.616e-06, 1.117e-06, 2.824e-06, 6.234e-08, 6.612e-07, 2.255e-07, 7.001e-08, 1.237e-08, 7.279e-08, 1.808e-07, 1.666e-07, 1.244e-07, 2.353e-08, 6.079e-08, 5.453e-08, 2.37e-07, 8.185e-09, 2.796e-06, 2.717e-07, 2.258e-07, 2.828e-07, 3.486e-07, 9.929e-08, 6.71e-07, 4.375e-07, 2.857e-07, 9.515e-08, 1.046e-06, 4.415e-07, 5.222e-07, 6.826e-07, 8.228e-08]

    Phase: traj.phases.phase0
        New Grid:
            Number of Segments = 37
            Segment Ends = [-1.0, -0.9667, -0.9333, -0.9, -0.8667, -0.8, -0.7833, -0.7667, -0.7333, -0.7, -0.6667, -0.6333, -0.6, -0.5333, -0.4667, -0.4, -0.3333, -0.2667, -0.2, -0.1333, -0.0667, 0.0667, 0.1333, 0.2, 0.2667, 0.3333, 0.4, 0.4667, 0.5333, 0.6, 0.6333, 0.6667, 0.7333, 0.8, 0.8667, 0.9333, 0.9667, 1.0]
            Segment Order = [5, 5, 7, 7, 13, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 11, 5, 5, 13, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 7, 5, 9, 5, 5]
        Refined: True


--- Constraint Report [traj] ---
    --- phase0 ---
        None

Model viewer data has already been recorded for Driver.

/usr/share/miniconda/envs/test/lib/python3.11/site-packages/openmdao/core/system.py:4357: OpenMDAOWarning:Calling `list_inputs` before `final_setup` will only display the default values of variables and will not show the result of any `set_val` calls.
/usr/share/miniconda/envs/test/lib/python3.11/site-packages/dymos/phase/phase.py:3056: OpenMDAOWarning:phase0.states:x0 specifies 'fix_final=True'. If the given restart file has a different final value this will overwrite the user-specified value
/usr/share/miniconda/envs/test/lib/python3.11/site-packages/dymos/phase/phase.py:3056: OpenMDAOWarning:phase0.states:x1 specifies 'fix_final=True'. If the given restart file has a different final value this will overwrite the user-specified value

Full total jacobian for problem 'problem7' was computed 3 times, taking 0.6655220249999729 seconds.
Total jacobian shape: (307, 449) 


Jacobian shape: (307, 449)  (2.93% nonzero)
FWD solves: 0   REV solves: 30
Total colors vs. total size: 30 vs 307  (90.23% improvement)

Sparsity computed using tolerance: 1e-25
Time to compute sparsity:   0.6655 sec
Time to compute coloring:   0.1654 sec
Memory to compute coloring:   0.0000 MB
Coloring created on: 2024-11-18 20:35:33

Optimization terminated successfully    (Exit mode 0)
            Current function value: 5.3585990068712395
            Iterations: 5
            Function evaluations: 6
            Gradient evaluations: 5
Optimization Complete
-----------------------------------


==================================================
          Grid Refinement - Iteration 5           
--------------------------------------------------
    Phase: traj.phases.phase0
        Refinement Options:
            Allow Refinement = True
            Tolerance = 1e-06
            Min Order = 3
            Max Order = 14
        Original Grid:
            Number of Segments = 37
            Segment Ends = [-1.0, -0.9667, -0.9333, -0.9, -0.8667, -0.8, -0.7833, -0.7667, -0.7333, -0.7, -0.6667, -0.6333, -0.6, -0.5333, -0.4667, -0.4, -0.3333, -0.2667, -0.2, -0.1333, -0.0667, 0.0667, 0.1333, 0.2, 0.2667, 0.3333, 0.4, 0.4667, 0.5333, 0.6, 0.6333, 0.6667, 0.7333, 0.8, 0.8667, 0.9333, 0.9667, 1.0]
            Segment Order = [5, 5, 7, 7, 13, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 11, 5, 5, 13, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 7, 5, 9, 5, 5]
            Error = [1.139e-06, 1.392e-06, 4.195e-07,  1.8e-07, 1.625e-07, 6.331e-07, 6.768e-08, 1.48e-09, 1.649e-06, 1.106e-06, 1.87e-07, 1.607e-08, 2.484e-07, 7.502e-08, 9.79e-08, 1.071e-07, 6.825e-08, 1.758e-08, 7.698e-08, 1.472e-07, 2.042e-07, 1.14e-06, 8.424e-07, 2.01e-07, 3.213e-07, 2.412e-07, 1.875e-07, 9.364e-08, 2.46e-07, 2.211e-07, 5.308e-07, 2.496e-06, 4.273e-08, 9.287e-07, 4.848e-09, 5.861e-07, 7.877e-07]

    Phase: traj.phases.phase0
        New Grid:
            Number of Segments = 38
            Segment Ends = [-1.0, -0.9667, -0.9333, -0.9, -0.8667, -0.8, -0.7833, -0.7667, -0.7333, -0.7, -0.6667, -0.6333, -0.6, -0.5333, -0.4667, -0.4, -0.3333, -0.2667, -0.2, -0.1333, -0.0667, 0.0667, 0.1333, 0.2, 0.2667, 0.3333, 0.4, 0.4667, 0.5333, 0.6, 0.6333, 0.6667, 0.7, 0.7333, 0.8, 0.8667, 0.9333, 0.9667, 1.0]
            Segment Order = [9, 11, 7, 7, 13, 5, 5, 5, 15, 9, 5, 5, 5, 5, 5, 5, 5, 11, 5, 5, 13, 9, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 7, 5, 9, 5, 5]
        Refined: True


--- Constraint Report [traj] ---
    --- phase0 ---
        None

Model viewer data has already been recorded for Driver.

/usr/share/miniconda/envs/test/lib/python3.11/site-packages/openmdao/core/system.py:4357: OpenMDAOWarning:Calling `list_inputs` before `final_setup` will only display the default values of variables and will not show the result of any `set_val` calls.
/usr/share/miniconda/envs/test/lib/python3.11/site-packages/dymos/phase/phase.py:3056: OpenMDAOWarning:phase0.states:x0 specifies 'fix_final=True'. If the given restart file has a different final value this will overwrite the user-specified value
/usr/share/miniconda/envs/test/lib/python3.11/site-packages/dymos/phase/phase.py:3056: OpenMDAOWarning:phase0.states:x1 specifies 'fix_final=True'. If the given restart file has a different final value this will overwrite the user-specified value

Full total jacobian for problem 'problem7' was computed 3 times, taking 0.8377432519999957 seconds.
Total jacobian shape: (356, 529) 

Jacobian shape: (356, 529)  (2.84% nonzero)
FWD solves: 0   REV solves: 36
Total colors vs. total size: 36 vs 356  (89.89% improvement)

Sparsity computed using tolerance: 1e-25
Time to compute sparsity:   0.8377 sec
Time to compute coloring:   0.2110 sec
Memory to compute coloring:   0.0000 MB
Coloring created on: 2024-11-18 20:35:36

Optimization terminated successfully    (Exit mode 0)
            Current function value: 5.358600622455051
            Iterations: 2
            Function evaluations: 3
            Gradient evaluations: 2
Optimization Complete
-----------------------------------
Successfully completed grid refinement.
==================================================

/usr/share/miniconda/envs/test/lib/python3.11/site-packages/openmdao/core/group.py:1137: DerivativesWarning:Constraints or objectives [ode_eval.control_interp.control_rates:u_rate, ode_eval.control_interp.control_rates:u_rate2, ode_eval.control_interp.control_values:u] cannot be impacted by the design variables of the problem because no partials were defined for them in their parent component(s).

Simulating trajectory traj
Model viewer data has already been recorded for Driver.

Done simulating trajectory traj

Problem: problem7
Driver:  ScipyOptimizeDriver
  success     : True
  iterations  : 4
  runtime     : 2.0704E+00 s
  model_evals : 4
  model_time  : 3.7605E-03 s
  deriv_evals : 2
  deriv_time  : 4.9706E-02 s
  exit_status : SUCCESS

(<Figure size 1000x800 with 5 Axes>,
 array([<Axes: xlabel='time (s)', ylabel='$x_1$ (V)'>,
        <Axes: xlabel='time (s)', ylabel='$x_0$ (V/s)'>,
        <Axes: xlabel='time (s)', ylabel='J'>,
        <Axes: xlabel='$x_0$ (V/s)', ylabel='$x_1$ (V)'>,
        <Axes: xlabel='time (s)', ylabel='control u'>], dtype=object))

../../_images/06a7723a6dfdf16404be9fb99374f60547709ccbdca5688b7a6e7405b14c5674.png

References#

[Wikipediacontributors20]

Wikipedia contributors. Van der pol oscillator — Wikipedia, the free encyclopedia. 2020. [Online; accessed 12-June-2020]. URL: https://en.wikipedia.org/w/index.php?title=Van_der_Pol_oscillator&oldid=953857769.