The Hull Problem

The Hull Problem#

The Hull problem is a 1-DOF optimal control problem [Hul03]. It can be stated as:

Minimize the control effort required to move a frictionless sliding block from some initial position such that the final displacement from a pre-specified point is minimized.

State and control variables#

This system has one state variables, the position (\(x\)) of the sliding block.

This system has a single control variable (\(u\)), the velocity of the block.

The dynamics of the system are governed by

(48)#\[\begin{align} \dot{x} &= u \end{align}\]

Problem Definition#

We seek to minimize the control effort required and minimize the displacement from the origin.

(49)#\[\begin{align} \mathrm{Minimize} \, J &= 2.5x_f^2 \, + \, 0.5 \int_0^1 u^2 dt \end{align}\]

Subject to the initial conditions

(50)#\[\begin{align} t_0 &= 0.0 \\ x_0 &= 1.5 \end{align}\]

and the terminal constraints

(51)#\[\begin{align} t_f &= 10.0 \end{align}\]

Dealing with combined terminal and integral costs in Dymos#

In classic optimal control, the objective is often broken into the terminal component (the Mayer term) and the integral component (the Lagrange term). Dymos does not distinguish between the two. In this case, since the objective \(J\) consists of both a terminal cost and an integrated cost (Bolza form), we add a term to the ODE to account for the integrated quantity

(52)#\[\begin{align} \dot{x_L} &= L \\ L &= 0.5 u^2 \end{align}\]

where \(x_L\) is a state added to account for the Lagrange term.

Dymos supports the definition of simple mathematical expressions as the cost, so the final value of \(x_L\) can be added to the final value of \(2.5x^2\).

Defining the ODE#

The following code implements the equations of motion for the Hull problem. Since the rate of \(x\) is given by a control (\(u\)), there is no need to compute its rate in the ODE. Dymos can pull their values from those other states and controls. The ODE, therefore, only needs to compute the rate of change of \(x_L\) (\(L\)).

A few things to note:

By providing the tag dymos.state_rate_source:{name}, we’re letting Dymos know what states need to be integrated, there’s no need to specify a rate source when using this ODE in our Phase.
Pairing the above tag with dymos.state_units:{units} means we don’t have to specify units when setting properties for the state in our run script.

import numpy as np
import openmdao.api as om


class HullProblemODE(om.ExplicitComponent):
    def initialize(self):
        self.options.declare('num_nodes', types=int)

    def setup(self):
        nn = self.options['num_nodes']

        self.add_input('u', val=np.zeros(nn), desc='control')

        self.add_output('L', val=np.zeros(nn), desc='Lagrangian', units='1/s')

        # Setup partials
        self.declare_partials(of='L', wrt='u', rows=np.arange(nn), cols=np.arange(nn))

    def compute(self, inputs, outputs, discrete_inputs=None, discrete_outputs=None):
        u = inputs['u']

        outputs['L'] = 0.5 * u ** 2

    def compute_partials(self, inputs, partials, discrete_inputs=None):
        u = inputs['u']
        partials['L', 'u'] = u

Solving the Hull problem with Dymos#

The following script solves the Hull problem with Dymos.

To begin, import the packages we require:

import dymos as dm
import matplotlib.pyplot as plt

We then instantiate an OpenMDAO problem and set the optimizer and its options.

The call to declare_coloring tells the optimizer to attempt to find a sparsity pattern that minimizes the work required to compute the derivatives across the model.

#
# Initialize the Problem and the optimization driver
#
p = om.Problem()
               
p.driver = om.pyOptSparseDriver()
p.driver.declare_coloring()

Next, we add a Dymos Trajectory group to the problem’s model and add a phase to it.

In this case we’re using the Radau pseudospectral transcription to solve the problem.

#
# Create a trajectory and add a phase to it
#
traj = p.model.add_subsystem('traj', dm.Trajectory())
tx = transcription = dm.Radau(num_segments=24)
phase = traj.add_phase('phase0', dm.Phase(ode_class=HullProblemODE, transcription=tx))

At this point, we set the options on the main variables used in a Dymos phase.

In addition to time, we have two states (x, and x_L) and a single control (u).

Here we use bounds on the states themselves to constrain the initial values of x and1 x_L. From an optimization perspective, this means that we are removing the first and last values in the state histories of \(x\) and \(x_L\) from the vector of design variables. Their initial values will remain unchanged throughout the optimization process.

On the other hand, we could specify fix_initial=False, fix_final=False for these values, and Dymos would be free to change them. We would then need to put a boundary constraint in place to enforce their final values. Feel free to experiment with different ways of enforcing the boundary constraints on this problem and see how it affects performance.

The scaler values (ref) are all set to 1 here.

Also, we don’t need to specify targets for any of the variables here because their names are the targets in the top-level of the model. The rate source and units for the states are obtained from the tags in the ODE component we previously defined.

#
# Set the variables
#
phase.set_time_options(fix_initial=True, fix_duration=True)

phase.set_time_options(fix_initial=True, fix_duration=True)
phase.add_state('x', fix_initial=True, fix_final=False, rate_source='u')
phase.add_state('xL', fix_initial=True, fix_final=False, rate_source='L')
phase.add_parameter('u', opt=True, targets=['u'], units='1/s')
phase.add_timeseries_output('u')

#
# Minimize time at the end of the phase
#
phase.add_objective('J = 2.5*x**2 + xL')

#
# Setup the Problem
#
p.setup()

<openmdao.core.problem.Problem at 0x7f87c6df7e00>

We then set the initial guesses for the variables in the problem and solve it.

We’re using the phase interp method to provide initial guesses for the states and controls. In this case, by giving it two values, it is linearly interpolating from the first value to the second value, and then returning the interpolated value at the input nodes for the given variable.

Finally, we use the dymos.run_problem method to execute the problem. This interface allows us to do some things that the standard OpenMDAO problem.run_driver interface does not. It will automatically record the final solution achieved by the optimizer in case named 'final' in a file called dymos_solution.db. By specifying simulate=True, it will automatically follow the solution with an explicit integration using scipy.solve_ivp. The results of the simulation are stored in a case named final in the file dymos_simulation.db. This explicit simulation demonstrates how the system evolved with the given controls, and serves as a check that we’re using a dense enough grid (enough segments and segments of sufficient order) to accurately represent the solution.

If those two solution didn’t agree reasonably well, we could rerun the problem with a more dense grid. Instead, we’re asking Dymos to automatically change the grid if necessary by specifying refine_method='ph'. This will attempt to repeatedly solve the problem and change the number of segments and segment orders until the solution is in reasonable agreement.

#
# Set the initial values
#
phase.set_state_val('x', [1.5, 1])
phase.set_state_val('xL', [0, 1])
phase.set_time_val(initial=0.0, duration=1.0)
phase.set_parameter_val('u', 0.7)

#
# Solve for the optimal trajectory
#
dm.run_problem(p, run_driver=True, simulate=True)

Show code cell output

Hide code cell output

/usr/share/miniconda/envs/test/lib/python3.13/site-packages/openmdao/core/group.py:3165: UnitsWarning:'traj.phases.phase0' <class Phase>: Output 'traj.phases.phase0.param_comp.parameter_vals:u' with units of '1/s' is connected to input 'traj.phases.phase0.rhs_all.user_ode.u' which has no units.

Jacobian shape: (145, 145)  (3.41% nonzero)
FWD solves: 5   REV solves: 0
Total colors vs. total size: 5 vs 145  (96.55% improvement)

Sparsity computed using tolerance: 1e-25.
Dense total jacobian for Problem 'problem' was computed 3 times.
Time to compute sparsity:   0.1517 sec
Time to compute coloring:   0.0970 sec
Memory to compute coloring:   0.3750 MB
Coloring created on: 2025-08-29 00:30:32

Optimization Problem -- Optimization using pyOpt_sparse
================================================================================
    Objective Function: _objfunc

    Solution: 
--------------------------------------------------------------------------------
    Total Time:                    0.6181
       User Objective Time :       0.0077
       User Sensitivity Time :     0.5004
       Interface Time :            0.0425
       Opt Solver Time:            0.0675
    Calls to Objective Function :      11
    Calls to Sens Function :           10


   Objectives
      Index  Name                             Value
          0  traj.phase0.rhs_all.J     9.375000E-01

   Variables (c - continuous, i - integer, d - discrete)
      Index  Name                         Type      Lower Bound            Value      Upper Bound     Status
          0  traj.phase0.parameters:u_0      c    -1.000000E+21    -1.250017E+00     1.000000E+21           
          1  traj.phase0.states:x_0          c    -1.000000E+21     1.481508E+00     1.000000E+21           
          2  traj.phase0.states:x_1          c    -1.000000E+21     1.455992E+00     1.000000E+21           
          3  traj.phase0.states:x_2          c    -1.000000E+21     1.447916E+00     1.000000E+21           
          4  traj.phase0.states:x_3          c    -1.000000E+21     1.429423E+00     1.000000E+21           
          5  traj.phase0.states:x_4          c    -1.000000E+21     1.403908E+00     1.000000E+21           
          6  traj.phase0.states:x_5          c    -1.000000E+21     1.395832E+00     1.000000E+21           
          7  traj.phase0.states:x_6          c    -1.000000E+21     1.377339E+00     1.000000E+21           
          8  traj.phase0.states:x_7          c    -1.000000E+21     1.351824E+00     1.000000E+21           
          9  traj.phase0.states:x_8          c    -1.000000E+21     1.343748E+00     1.000000E+21           
         10  traj.phase0.states:x_9          c    -1.000000E+21     1.325255E+00     1.000000E+21           
         11  traj.phase0.states:x_10         c    -1.000000E+21     1.299739E+00     1.000000E+21           
         12  traj.phase0.states:x_11         c    -1.000000E+21     1.291664E+00     1.000000E+21           
         13  traj.phase0.states:x_12         c    -1.000000E+21     1.273171E+00     1.000000E+21           
         14  traj.phase0.states:x_13         c    -1.000000E+21     1.247655E+00     1.000000E+21           
         15  traj.phase0.states:x_14         c    -1.000000E+21     1.239580E+00     1.000000E+21           
         16  traj.phase0.states:x_15         c    -1.000000E+21     1.221087E+00     1.000000E+21           
         17  traj.phase0.states:x_16         c    -1.000000E+21     1.195571E+00     1.000000E+21           
         18  traj.phase0.states:x_17         c    -1.000000E+21     1.187496E+00     1.000000E+21           
         19  traj.phase0.states:x_18         c    -1.000000E+21     1.169003E+00     1.000000E+21           
         20  traj.phase0.states:x_19         c    -1.000000E+21     1.143487E+00     1.000000E+21           
         21  traj.phase0.states:x_20         c    -1.000000E+21     1.135412E+00     1.000000E+21           
         22  traj.phase0.states:x_21         c    -1.000000E+21     1.116919E+00     1.000000E+21           
         23  traj.phase0.states:x_22         c    -1.000000E+21     1.091403E+00     1.000000E+21           
         24  traj.phase0.states:x_23         c    -1.000000E+21     1.083328E+00     1.000000E+21           
         25  traj.phase0.states:x_24         c    -1.000000E+21     1.064835E+00     1.000000E+21           
         26  traj.phase0.states:x_25         c    -1.000000E+21     1.039319E+00     1.000000E+21           
         27  traj.phase0.states:x_26         c    -1.000000E+21     1.031244E+00     1.000000E+21           
         28  traj.phase0.states:x_27         c    -1.000000E+21     1.012751E+00     1.000000E+21           
         29  traj.phase0.states:x_28         c    -1.000000E+21     9.872351E-01     1.000000E+21           
         30  traj.phase0.states:x_29         c    -1.000000E+21     9.791594E-01     1.000000E+21           
         31  traj.phase0.states:x_30         c    -1.000000E+21     9.606669E-01     1.000000E+21           
         32  traj.phase0.states:x_31         c    -1.000000E+21     9.351511E-01     1.000000E+21           
         33  traj.phase0.states:x_32         c    -1.000000E+21     9.270754E-01     1.000000E+21           
         34  traj.phase0.states:x_33         c    -1.000000E+21     9.085829E-01     1.000000E+21           
         35  traj.phase0.states:x_34         c    -1.000000E+21     8.830670E-01     1.000000E+21           
         36  traj.phase0.states:x_35         c    -1.000000E+21     8.749913E-01     1.000000E+21           
         37  traj.phase0.states:x_36         c    -1.000000E+21     8.564988E-01     1.000000E+21           
         38  traj.phase0.states:x_37         c    -1.000000E+21     8.309830E-01     1.000000E+21           
         39  traj.phase0.states:x_38         c    -1.000000E+21     8.229073E-01     1.000000E+21           
         40  traj.phase0.states:x_39         c    -1.000000E+21     8.044148E-01     1.000000E+21           
         41  traj.phase0.states:x_40         c    -1.000000E+21     7.788989E-01     1.000000E+21           
         42  traj.phase0.states:x_41         c    -1.000000E+21     7.708232E-01     1.000000E+21           
         43  traj.phase0.states:x_42         c    -1.000000E+21     7.523307E-01     1.000000E+21           
         44  traj.phase0.states:x_43         c    -1.000000E+21     7.268149E-01     1.000000E+21           
         45  traj.phase0.states:x_44         c    -1.000000E+21     7.187392E-01     1.000000E+21           
         46  traj.phase0.states:x_45         c    -1.000000E+21     7.002467E-01     1.000000E+21           
         47  traj.phase0.states:x_46         c    -1.000000E+21     6.747308E-01     1.000000E+21           
         48  traj.phase0.states:x_47         c    -1.000000E+21     6.666551E-01     1.000000E+21           
         49  traj.phase0.states:x_48         c    -1.000000E+21     6.481626E-01     1.000000E+21           
         50  traj.phase0.states:x_49         c    -1.000000E+21     6.226467E-01     1.000000E+21           
         51  traj.phase0.states:x_50         c    -1.000000E+21     6.145711E-01     1.000000E+21           
         52  traj.phase0.states:x_51         c    -1.000000E+21     5.960786E-01     1.000000E+21           
         53  traj.phase0.states:x_52         c    -1.000000E+21     5.705627E-01     1.000000E+21           
         54  traj.phase0.states:x_53         c    -1.000000E+21     5.624870E-01     1.000000E+21           
         55  traj.phase0.states:x_54         c    -1.000000E+21     5.439945E-01     1.000000E+21           
         56  traj.phase0.states:x_55         c    -1.000000E+21     5.184786E-01     1.000000E+21           
         57  traj.phase0.states:x_56         c    -1.000000E+21     5.104029E-01     1.000000E+21           
         58  traj.phase0.states:x_57         c    -1.000000E+21     4.919104E-01     1.000000E+21           
         59  traj.phase0.states:x_58         c    -1.000000E+21     4.663946E-01     1.000000E+21           
         60  traj.phase0.states:x_59         c    -1.000000E+21     4.583189E-01     1.000000E+21           
         61  traj.phase0.states:x_60         c    -1.000000E+21     4.398264E-01     1.000000E+21           
         62  traj.phase0.states:x_61         c    -1.000000E+21     4.143105E-01     1.000000E+21           
         63  traj.phase0.states:x_62         c    -1.000000E+21     4.062348E-01     1.000000E+21           
         64  traj.phase0.states:x_63         c    -1.000000E+21     3.877423E-01     1.000000E+21           
         65  traj.phase0.states:x_64         c    -1.000000E+21     3.622265E-01     1.000000E+21           
         66  traj.phase0.states:x_65         c    -1.000000E+21     3.541508E-01     1.000000E+21           
         67  traj.phase0.states:x_66         c    -1.000000E+21     3.356583E-01     1.000000E+21           
         68  traj.phase0.states:x_67         c    -1.000000E+21     3.101424E-01     1.000000E+21           
         69  traj.phase0.states:x_68         c    -1.000000E+21     3.020667E-01     1.000000E+21           
         70  traj.phase0.states:x_69         c    -1.000000E+21     2.835742E-01     1.000000E+21           
         71  traj.phase0.states:x_70         c    -1.000000E+21     2.580584E-01     1.000000E+21           
         72  traj.phase0.states:x_71         c    -1.000000E+21     2.499827E-01     1.000000E+21           
         73  traj.phase0.states:xL_0         c    -1.000000E+21     1.155797E-02     1.000000E+21           
         74  traj.phase0.states:xL_1         c    -1.000000E+21     2.750561E-02     1.000000E+21           
         75  traj.phase0.states:xL_2         c    -1.000000E+21     3.255299E-02     1.000000E+21           
         76  traj.phase0.states:xL_3         c    -1.000000E+21     4.411096E-02     1.000000E+21           
         77  traj.phase0.states:xL_4         c    -1.000000E+21     6.005860E-02     1.000000E+21           
         78  traj.phase0.states:xL_5         c    -1.000000E+21     6.510597E-02     1.000000E+21           
         79  traj.phase0.states:xL_6         c    -1.000000E+21     7.666394E-02     1.000000E+21           
         80  traj.phase0.states:xL_7         c    -1.000000E+21     9.261158E-02     1.000000E+21           
         81  traj.phase0.states:xL_8         c    -1.000000E+21     9.765896E-02     1.000000E+21           
         82  traj.phase0.states:xL_9         c    -1.000000E+21     1.092169E-01     1.000000E+21           
         83  traj.phase0.states:xL_10        c    -1.000000E+21     1.251646E-01     1.000000E+21           
         84  traj.phase0.states:xL_11        c    -1.000000E+21     1.302119E-01     1.000000E+21           
         85  traj.phase0.states:xL_12        c    -1.000000E+21     1.417699E-01     1.000000E+21           
         86  traj.phase0.states:xL_13        c    -1.000000E+21     1.577176E-01     1.000000E+21           
         87  traj.phase0.states:xL_14        c    -1.000000E+21     1.627649E-01     1.000000E+21           
         88  traj.phase0.states:xL_15        c    -1.000000E+21     1.743229E-01     1.000000E+21           
         89  traj.phase0.states:xL_16        c    -1.000000E+21     1.902705E-01     1.000000E+21           
         90  traj.phase0.states:xL_17        c    -1.000000E+21     1.953179E-01     1.000000E+21           
         91  traj.phase0.states:xL_18        c    -1.000000E+21     2.068759E-01     1.000000E+21           
         92  traj.phase0.states:xL_19        c    -1.000000E+21     2.228235E-01     1.000000E+21           
         93  traj.phase0.states:xL_20        c    -1.000000E+21     2.278709E-01     1.000000E+21           
         94  traj.phase0.states:xL_21        c    -1.000000E+21     2.394289E-01     1.000000E+21           
         95  traj.phase0.states:xL_22        c    -1.000000E+21     2.553765E-01     1.000000E+21           
         96  traj.phase0.states:xL_23        c    -1.000000E+21     2.604239E-01     1.000000E+21           
         97  traj.phase0.states:xL_24        c    -1.000000E+21     2.719819E-01     1.000000E+21           
         98  traj.phase0.states:xL_25        c    -1.000000E+21     2.879295E-01     1.000000E+21           
         99  traj.phase0.states:xL_26        c    -1.000000E+21     2.929769E-01     1.000000E+21           
        100  traj.phase0.states:xL_27        c    -1.000000E+21     3.045348E-01     1.000000E+21           
        101  traj.phase0.states:xL_28        c    -1.000000E+21     3.204825E-01     1.000000E+21           
        102  traj.phase0.states:xL_29        c    -1.000000E+21     3.255299E-01     1.000000E+21           
        103  traj.phase0.states:xL_30        c    -1.000000E+21     3.370878E-01     1.000000E+21           
        104  traj.phase0.states:xL_31        c    -1.000000E+21     3.530355E-01     1.000000E+21           
        105  traj.phase0.states:xL_32        c    -1.000000E+21     3.580828E-01     1.000000E+21           
        106  traj.phase0.states:xL_33        c    -1.000000E+21     3.696408E-01     1.000000E+21           
        107  traj.phase0.states:xL_34        c    -1.000000E+21     3.855885E-01     1.000000E+21           
        108  traj.phase0.states:xL_35        c    -1.000000E+21     3.906358E-01     1.000000E+21           
        109  traj.phase0.states:xL_36        c    -1.000000E+21     4.021938E-01     1.000000E+21           
        110  traj.phase0.states:xL_37        c    -1.000000E+21     4.181414E-01     1.000000E+21           
        111  traj.phase0.states:xL_38        c    -1.000000E+21     4.231888E-01     1.000000E+21           
        112  traj.phase0.states:xL_39        c    -1.000000E+21     4.347468E-01     1.000000E+21           
        113  traj.phase0.states:xL_40        c    -1.000000E+21     4.506944E-01     1.000000E+21           
        114  traj.phase0.states:xL_41        c    -1.000000E+21     4.557418E-01     1.000000E+21           
        115  traj.phase0.states:xL_42        c    -1.000000E+21     4.672998E-01     1.000000E+21           
        116  traj.phase0.states:xL_43        c    -1.000000E+21     4.832474E-01     1.000000E+21           
        117  traj.phase0.states:xL_44        c    -1.000000E+21     4.882948E-01     1.000000E+21           
        118  traj.phase0.states:xL_45        c    -1.000000E+21     4.998528E-01     1.000000E+21           
        119  traj.phase0.states:xL_46        c    -1.000000E+21     5.158004E-01     1.000000E+21           
        120  traj.phase0.states:xL_47        c    -1.000000E+21     5.208478E-01     1.000000E+21           
        121  traj.phase0.states:xL_48        c    -1.000000E+21     5.324057E-01     1.000000E+21           
        122  traj.phase0.states:xL_49        c    -1.000000E+21     5.483534E-01     1.000000E+21           
        123  traj.phase0.states:xL_50        c    -1.000000E+21     5.534008E-01     1.000000E+21           
        124  traj.phase0.states:xL_51        c    -1.000000E+21     5.649587E-01     1.000000E+21           
        125  traj.phase0.states:xL_52        c    -1.000000E+21     5.809064E-01     1.000000E+21           
        126  traj.phase0.states:xL_53        c    -1.000000E+21     5.859537E-01     1.000000E+21           
        127  traj.phase0.states:xL_54        c    -1.000000E+21     5.975117E-01     1.000000E+21           
        128  traj.phase0.states:xL_55        c    -1.000000E+21     6.134594E-01     1.000000E+21           
        129  traj.phase0.states:xL_56        c    -1.000000E+21     6.185067E-01     1.000000E+21           
        130  traj.phase0.states:xL_57        c    -1.000000E+21     6.300647E-01     1.000000E+21           
        131  traj.phase0.states:xL_58        c    -1.000000E+21     6.460123E-01     1.000000E+21           
        132  traj.phase0.states:xL_59        c    -1.000000E+21     6.510597E-01     1.000000E+21           
        133  traj.phase0.states:xL_60        c    -1.000000E+21     6.626177E-01     1.000000E+21           
        134  traj.phase0.states:xL_61        c    -1.000000E+21     6.785653E-01     1.000000E+21           
        135  traj.phase0.states:xL_62        c    -1.000000E+21     6.836127E-01     1.000000E+21           
        136  traj.phase0.states:xL_63        c    -1.000000E+21     6.951707E-01     1.000000E+21           
        137  traj.phase0.states:xL_64        c    -1.000000E+21     7.111183E-01     1.000000E+21           
        138  traj.phase0.states:xL_65        c    -1.000000E+21     7.161657E-01     1.000000E+21           
        139  traj.phase0.states:xL_66        c    -1.000000E+21     7.277237E-01     1.000000E+21           
        140  traj.phase0.states:xL_67        c    -1.000000E+21     7.436713E-01     1.000000E+21           
        141  traj.phase0.states:xL_68        c    -1.000000E+21     7.487187E-01     1.000000E+21           
        142  traj.phase0.states:xL_69        c    -1.000000E+21     7.602766E-01     1.000000E+21           
        143  traj.phase0.states:xL_70        c    -1.000000E+21     7.762243E-01     1.000000E+21           
        144  traj.phase0.states:xL_71        c    -1.000000E+21     7.812717E-01     1.000000E+21           

   Constraints (i - inequality, e - equality)
      Index  Name                                          Type          Lower           Value           Upper    Status  Lagrange Multiplier (N/A)
          0  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    2.266705E-16    0.000000E+00              9.00000E+100
          1  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -2.174187E-16    0.000000E+00              9.00000E+100
          2  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -2.174187E-16    0.000000E+00              9.00000E+100
          3  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -2.544261E-16    0.000000E+00              9.00000E+100
          4  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    1.896631E-16    0.000000E+00              9.00000E+100
          5  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -2.544261E-16    0.000000E+00              9.00000E+100
          6  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    6.707597E-16    0.000000E+00              9.00000E+100
          7  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -2.174187E-16    0.000000E+00              9.00000E+100
          8  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -2.174187E-16    0.000000E+00              9.00000E+100
          9  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -2.544261E-16    0.000000E+00              9.00000E+100
         10  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    4.117077E-16    0.000000E+00              9.00000E+100
         11  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -2.544261E-16    0.000000E+00              9.00000E+100
         12  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -2.174187E-16    0.000000E+00              9.00000E+100
         13  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    2.266705E-16    0.000000E+00              9.00000E+100
         14  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -2.174187E-16    0.000000E+00              9.00000E+100
         15  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    1.780983E-15    0.000000E+00              9.00000E+100
         16  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -4.394633E-16    0.000000E+00              9.00000E+100
         17  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    2.266705E-16    0.000000E+00              9.00000E+100
         18  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    1.896631E-16    0.000000E+00              9.00000E+100
         19  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    1.896631E-16    0.000000E+00              9.00000E+100
         20  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    1.896631E-16    0.000000E+00              9.00000E+100
         21  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -2.174187E-16    0.000000E+00              9.00000E+100
         22  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    1.156482E-16    0.000000E+00              9.00000E+100
         23  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    2.266705E-16    0.000000E+00              9.00000E+100
         24  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    2.266705E-16    0.000000E+00              9.00000E+100
         25  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    1.156482E-16    0.000000E+00              9.00000E+100
         26  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -6.615079E-16    0.000000E+00              9.00000E+100
         27  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    6.337523E-16    0.000000E+00              9.00000E+100
         28  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -3.238150E-17    0.000000E+00              9.00000E+100
         29  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -2.544261E-16    0.000000E+00              9.00000E+100
         30  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -4.394633E-16    0.000000E+00              9.00000E+100
         31  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    4.625929E-18    0.000000E+00              9.00000E+100
         32  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    4.625929E-18    0.000000E+00              9.00000E+100
         33  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -6.615079E-16    0.000000E+00              9.00000E+100
         34  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    4.625929E-18    0.000000E+00              9.00000E+100
         35  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    4.625929E-18    0.000000E+00              9.00000E+100
         36  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    1.896631E-16    0.000000E+00              9.00000E+100
         37  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    7.864080E-17    0.000000E+00              9.00000E+100
         38  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -3.238150E-17    0.000000E+00              9.00000E+100
         39  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -6.985153E-16    0.000000E+00              9.00000E+100
         40  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -3.238150E-17    0.000000E+00              9.00000E+100
         41  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    4.117077E-16    0.000000E+00              9.00000E+100
         42  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -1.850372E-16    0.000000E+00              9.00000E+100
         43  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    1.480297E-16    0.000000E+00              9.00000E+100
         44  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    2.590520E-16    0.000000E+00              9.00000E+100
         45  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -4.764707E-16    0.000000E+00              9.00000E+100
         46  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -3.238150E-17    0.000000E+00              9.00000E+100
         47  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    1.896631E-16    0.000000E+00              9.00000E+100
         48  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    4.117077E-16    0.000000E+00              9.00000E+100
         49  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -3.238150E-17    0.000000E+00              9.00000E+100
         50  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -3.238150E-17    0.000000E+00              9.00000E+100
         51  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -6.291264E-16    0.000000E+00              9.00000E+100
         52  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    3.145632E-16    0.000000E+00              9.00000E+100
         53  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -1.850372E-16    0.000000E+00              9.00000E+100
         54  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    1.896631E-16    0.000000E+00              9.00000E+100
         55  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    7.864080E-17    0.000000E+00              9.00000E+100
         56  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    1.896631E-16    0.000000E+00              9.00000E+100
         57  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    7.864080E-17    0.000000E+00              9.00000E+100
         58  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -8.789266E-17    0.000000E+00              9.00000E+100
         59  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -1.434038E-16    0.000000E+00              9.00000E+100
         60  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -6.291264E-16    0.000000E+00              9.00000E+100
         61  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    9.251859E-17    0.000000E+00              9.00000E+100
         62  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -7.401487E-17    0.000000E+00              9.00000E+100
         63  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -4.764707E-16    0.000000E+00              9.00000E+100
         64  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -3.238150E-17    0.000000E+00              9.00000E+100
         65  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    1.896631E-16    0.000000E+00              9.00000E+100
         66  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -1.434038E-16    0.000000E+00              9.00000E+100
         67  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -3.238150E-17    0.000000E+00              9.00000E+100
         68  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -1.434038E-16    0.000000E+00              9.00000E+100
         69  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    3.700743E-17    0.000000E+00              9.00000E+100
         70  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00   -1.850372E-17    0.000000E+00              9.00000E+100
         71  traj.phase0.collocation_constraint.defects:x     e   0.000000E+00    3.700743E-17    0.000000E+00              9.00000E+100
         72  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301798E-11    0.000000E+00              9.00000E+100
         73  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301799E-11    0.000000E+00              9.00000E+100
         74  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301801E-11    0.000000E+00              9.00000E+100
         75  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301796E-11    0.000000E+00              9.00000E+100
         76  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301799E-11    0.000000E+00              9.00000E+100
         77  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301797E-11    0.000000E+00              9.00000E+100
         78  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301804E-11    0.000000E+00              9.00000E+100
         79  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301799E-11    0.000000E+00              9.00000E+100
         80  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301801E-11    0.000000E+00              9.00000E+100
         81  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301802E-11    0.000000E+00              9.00000E+100
         82  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301802E-11    0.000000E+00              9.00000E+100
         83  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301802E-11    0.000000E+00              9.00000E+100
         84  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301804E-11    0.000000E+00              9.00000E+100
         85  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301798E-11    0.000000E+00              9.00000E+100
         86  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301804E-11    0.000000E+00              9.00000E+100
         87  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301798E-11    0.000000E+00              9.00000E+100
         88  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301795E-11    0.000000E+00              9.00000E+100
         89  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301809E-11    0.000000E+00              9.00000E+100
         90  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301796E-11    0.000000E+00              9.00000E+100
         91  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301796E-11    0.000000E+00              9.00000E+100
         92  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301807E-11    0.000000E+00              9.00000E+100
         93  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301798E-11    0.000000E+00              9.00000E+100
         94  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301798E-11    0.000000E+00              9.00000E+100
         95  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301798E-11    0.000000E+00              9.00000E+100
         96  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301798E-11    0.000000E+00              9.00000E+100
         97  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301804E-11    0.000000E+00              9.00000E+100
         98  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301809E-11    0.000000E+00              9.00000E+100
         99  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301779E-11    0.000000E+00              9.00000E+100
        100  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301796E-11    0.000000E+00              9.00000E+100
        101  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301807E-11    0.000000E+00              9.00000E+100
        102  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301809E-11    0.000000E+00              9.00000E+100
        103  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301792E-11    0.000000E+00              9.00000E+100
        104  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301798E-11    0.000000E+00              9.00000E+100
        105  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301798E-11    0.000000E+00              9.00000E+100
        106  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301804E-11    0.000000E+00              9.00000E+100
        107  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301798E-11    0.000000E+00              9.00000E+100
        108  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301829E-11    0.000000E+00              9.00000E+100
        109  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301802E-11    0.000000E+00              9.00000E+100
        110  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301807E-11    0.000000E+00              9.00000E+100
        111  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301796E-11    0.000000E+00              9.00000E+100
        112  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301802E-11    0.000000E+00              9.00000E+100
        113  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301796E-11    0.000000E+00              9.00000E+100
        114  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301811E-11    0.000000E+00              9.00000E+100
        115  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301806E-11    0.000000E+00              9.00000E+100
        116  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301800E-11    0.000000E+00              9.00000E+100
        117  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301807E-11    0.000000E+00              9.00000E+100
        118  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301785E-11    0.000000E+00              9.00000E+100
        119  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301796E-11    0.000000E+00              9.00000E+100
        120  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301840E-11    0.000000E+00              9.00000E+100
        121  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301802E-11    0.000000E+00              9.00000E+100
        122  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301796E-11    0.000000E+00              9.00000E+100
        123  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301756E-11    0.000000E+00              9.00000E+100
        124  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301823E-11    0.000000E+00              9.00000E+100
        125  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301778E-11    0.000000E+00              9.00000E+100
        126  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301796E-11    0.000000E+00              9.00000E+100
        127  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301807E-11    0.000000E+00              9.00000E+100
        128  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301796E-11    0.000000E+00              9.00000E+100
        129  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301851E-11    0.000000E+00              9.00000E+100
        130  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301796E-11    0.000000E+00              9.00000E+100
        131  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301796E-11    0.000000E+00              9.00000E+100
        132  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301778E-11    0.000000E+00              9.00000E+100
        133  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301789E-11    0.000000E+00              9.00000E+100
        134  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301800E-11    0.000000E+00              9.00000E+100
        135  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301774E-11    0.000000E+00              9.00000E+100
        136  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301807E-11    0.000000E+00              9.00000E+100
        137  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301796E-11    0.000000E+00              9.00000E+100
        138  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301818E-11    0.000000E+00              9.00000E+100
        139  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301774E-11    0.000000E+00              9.00000E+100
        140  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301818E-11    0.000000E+00              9.00000E+100
        141  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301867E-11    0.000000E+00              9.00000E+100
        142  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301789E-11    0.000000E+00              9.00000E+100
        143  traj.phase0.collocation_constraint.defects:xL    e   0.000000E+00   -4.301823E-11    0.000000E+00              9.00000E+100


   Exit Status
      Inform  Description
           0  Optimization terminated successfully.
--------------------------------------------------------------------------------

Simulating trajectory traj
Done simulating trajectory traj

Problem: problem
Driver:  pyOptSparseDriver
  success     : True
  iterations  : 12
  runtime     : 9.2999E-01 s
  model_evals : 12
  model_time  : 4.9286E-03 s
  deriv_evals : 10
  deriv_time  : 3.7373E-02 s
  exit_status : SUCCESS

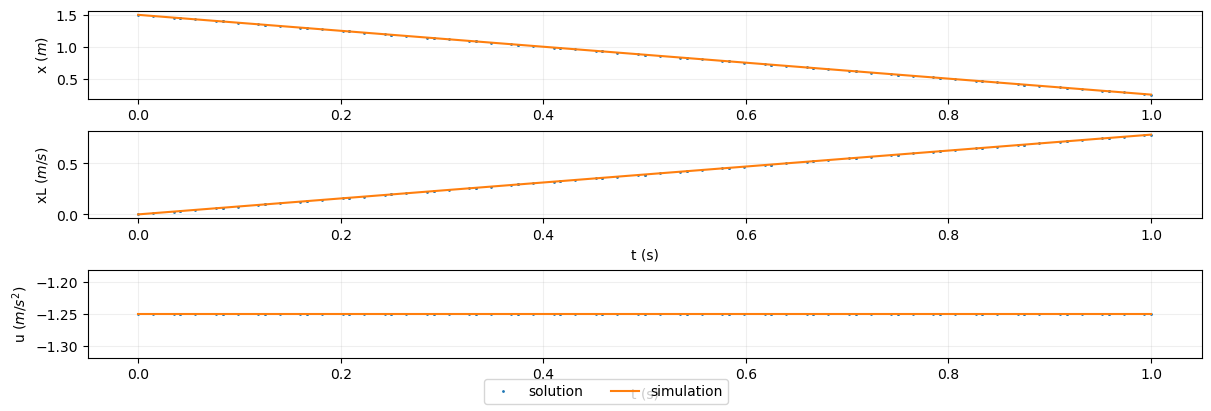
Plotting the solution#

The recommended practice is to obtain values from the recorded cases. While the problem object can also be queried for values, building plotting scripts that use the case recorder files as the data source means that the problem doesn’t need to be solved just to change a plot. Here we load values of various variables from the solution and simulation for use in the animation to follow.

sol = om.CaseReader(p.get_outputs_dir() / 'dymos_solution.db').get_case('final')
sim = om.CaseReader(traj.sim_prob.get_outputs_dir() / 'dymos_simulation.db').get_case('final')

t = sol.get_val('traj.phase0.timeseries.time')
x = sol.get_val('traj.phase0.timeseries.x')
xL = sol.get_val('traj.phase0.timeseries.xL')
u = sol.get_val('traj.phase0.timeseries.u')

t_sim = sim.get_val('traj.phase0.timeseries.time')
x_sim = sim.get_val('traj.phase0.timeseries.x')
xL_sim = sim.get_val('traj.phase0.timeseries.xL')
u_sim = sim.get_val('traj.phase0.timeseries.u')

fig = plt.figure(constrained_layout=True, figsize=(12, 4))
gs = fig.add_gridspec(3, 1)

x_ax = fig.add_subplot(gs[0, 0])
xL_ax = fig.add_subplot(gs[1, 0])
u_ax = fig.add_subplot(gs[2, 0])

x_ax.set_ylabel('x ($m$)')
xL_ax.set_ylabel('xL ($m/s$)')
u_ax.set_ylabel('u ($m/s^2$)')
xL_ax.set_xlabel('t (s)')
u_ax.set_xlabel('t (s)')

x_sol_handle, = x_ax.plot(t, x, 'o', ms=1)
xL_ax.plot(t, xL, 'o', ms=1)
u_ax.plot(t, u, 'o', ms=1)

x_sim_handle, = x_ax.plot(t_sim, x_sim, '-', ms=1)
xL_ax.plot(t_sim, xL_sim, '-', ms=1)
u_ax.plot(t_sim, u_sim, '-', ms=1)

for ax in [x_ax, xL_ax, u_ax]:
    ax.grid(True, alpha=0.2)
    
plt.figlegend([x_sol_handle, x_sim_handle], ['solution', 'simulation'], ncol=2, loc='lower center');

../../_images/93a1f3c3edbb9e10831213237863f46e6ceca6e344de9ad115a7904c103e947d.png

References#

[Hul03]

David G Hull. Optimal Control Theory for Applications. Springer, 2003.