The Brachistochrone with Externally-Sourced Controls#
Things you’ll learn through this example
How to provide trajectory control values from an external source.
This example is the same as the other brachistochrone example with one exception: the control values come from an external source upstream of the trajectory.
The following script fully defines the brachistochrone problem with Dymos and solves it.
A new IndepVarComp is added before the trajectory.
The transcription used in the relevant phase is defined first so that we can obtain the number of control input nodes.
The IndepVarComp then provides the control \(\theta\) at the correct number of nodes, and sends them to the trajectory.
Since the control values are no longer managed by Dymos, they are added as design variables using the OpenMDAO add_design_var method.
Show code cell outputs
import numpy as np
import openmdao.api as om
class BrachistochroneODE(om.ExplicitComponent):
def initialize(self):
self.options.declare('num_nodes', types=int)
self.options.declare('g', default=9.80665, desc='gravitational acceleration in m/s**2')
def setup(self):
nn = self.options['num_nodes']
# Inputs
self.add_input('v', val=np.zeros(nn), desc='velocity', units='m/s')
self.add_input('theta', val=np.ones(nn), desc='angle of wire', units='rad')
self.add_output('xdot', val=np.zeros(nn), desc='velocity component in x', units='m/s',
tags=['dymos.state_rate_source:x', 'dymos.state_units:m'])
self.add_output('ydot', val=np.zeros(nn), desc='velocity component in y', units='m/s',
tags=['dymos.state_rate_source:y', 'dymos.state_units:m'])
self.add_output('vdot', val=np.zeros(nn), desc='acceleration magnitude', units='m/s**2',
tags=['dymos.state_rate_source:v', 'dymos.state_units:m/s'])
self.add_output('check', val=np.zeros(nn), desc='check solution: v/sin(theta) = constant',
units='m/s')
# Setup partials
ar = np.arange(self.options['num_nodes'], dtype=int)
self.declare_partials(of='vdot', wrt='theta', rows=ar, cols=ar)
self.declare_partials(of='xdot', wrt='v', rows=ar, cols=ar)
self.declare_partials(of='xdot', wrt='theta', rows=ar, cols=ar)
self.declare_partials(of='ydot', wrt='v', rows=ar, cols=ar)
self.declare_partials(of='ydot', wrt='theta', rows=ar, cols=ar)
self.declare_partials(of='check', wrt='v', rows=ar, cols=ar)
self.declare_partials(of='check', wrt='theta', rows=ar, cols=ar)
def compute(self, inputs, outputs):
theta = inputs['theta']
cos_theta = np.cos(theta)
sin_theta = np.sin(theta)
g = self.options['g']
v = inputs['v']
outputs['vdot'] = g * cos_theta
outputs['xdot'] = v * sin_theta
outputs['ydot'] = -v * cos_theta
outputs['check'] = v / sin_theta
def compute_partials(self, inputs, partials):
theta = inputs['theta']
cos_theta = np.cos(theta)
sin_theta = np.sin(theta)
g = self.options['g']
v = inputs['v']
partials['vdot', 'theta'] = -g * sin_theta
partials['xdot', 'v'] = sin_theta
partials['xdot', 'theta'] = v * cos_theta
partials['ydot', 'v'] = -cos_theta
partials['ydot', 'theta'] = v * sin_theta
partials['check', 'v'] = 1 / sin_theta
partials['check', 'theta'] = -v * cos_theta / sin_theta**2
import numpy as np
import openmdao.api as om
import dymos as dm
import matplotlib.pyplot as plt
from dymos.examples.brachistochrone.brachistochrone_ode import BrachistochroneODE
#
# Define the OpenMDAO problem
#
p = om.Problem(model=om.Group())
# Instantiate the transcription so we can get the number of nodes from it while
# building the problem.
tx = dm.GaussLobatto(num_segments=10, order=3)
# Add an indep var comp to provide the external control values
ivc = p.model.add_subsystem('control_ivc', om.IndepVarComp(), promotes_outputs=['*'])
# Add the output to provide the values of theta at the control input nodes of the transcription.
ivc.add_output('theta', shape=(tx.grid_data.subset_num_nodes['control_input']), units='rad')
# Add this external control as a design variable
p.model.add_design_var('theta', units='rad', lower=1.0E-5, upper=np.pi)
# Connect this to controls:theta in the appropriate phase.
# connect calls are cached, so we can do this before we actually add the trajectory to the problem.
p.model.connect('theta', 'traj.phase0.controls:theta')
#
# Define a Trajectory object
#
traj = dm.Trajectory()
p.model.add_subsystem('traj', subsys=traj)
#
# Define a Dymos Phase object with GaussLobatto Transcription
#
phase = dm.Phase(ode_class=BrachistochroneODE,
transcription=tx)
traj.add_phase(name='phase0', phase=phase)
#
# Set the time options
# Time has no targets in our ODE.
# We fix the initial time so that the it is not a design variable in the optimization.
# The duration of the phase is allowed to be optimized, but is bounded on [0.5, 10].
#
phase.set_time_options(fix_initial=True, duration_bounds=(0.5, 10.0), units='s')
#
# Set the time options
# Initial values of positions and velocity are all fixed.
# The final value of position are fixed, but the final velocity is a free variable.
# The equations of motion are not functions of position, so 'x' and 'y' have no targets.
# The rate source points to the output in the ODE which provides the time derivative of the
# given state.
phase.add_state('x', fix_initial=True, fix_final=True, units='m', rate_source='xdot')
phase.add_state('y', fix_initial=True, fix_final=True, units='m', rate_source='ydot')
phase.add_state('v', fix_initial=True, fix_final=False, units='m/s',
rate_source='vdot', targets=['v'])
# Define theta as a control.
# Use opt=False to allow it to be connected to an external source.
# Arguments lower and upper are no longer valid for an input control.
phase.add_control(name='theta', targets=['theta'], opt=False)
# Minimize final time.
phase.add_objective('time', loc='final')
# Set the driver.
p.driver = om.ScipyOptimizeDriver()
# Allow OpenMDAO to automatically determine our sparsity pattern.
# Doing so can significant speed up the execution of Dymos.
p.driver.declare_coloring()
# Setup the problem
p.setup(check=True)
# Now that the OpenMDAO problem is setup, we can set the values of the states and controls.
p.set_val('traj.phase0.states:x', phase.interp('x', [0, 10]), units='m')
p.set_val('traj.phase0.states:y', phase.interp('y', [10, 5]), units='m')
p.set_val('traj.phase0.states:v', phase.interp('v', [0, 5]), units='m/s')
p.set_val('traj.phase0.controls:theta', phase.interp('theta', [90, 90]), units='deg')
# Run the driver to solve the problem
p.run_driver()
# Test the results
print(p.get_val('traj.phase0.timeseries.time')[-1])
# Check the validity of our results by using scipy.integrate.solve_ivp to
# integrate the solution.
sim_out = traj.simulate()
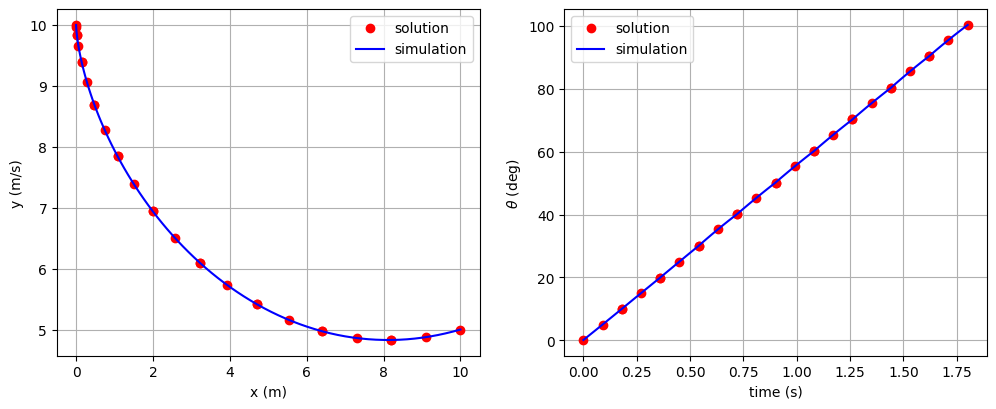
# Plot the results
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(12, 4.5))
axes[0].plot(p.get_val('traj.phase0.timeseries.states:x'),
p.get_val('traj.phase0.timeseries.states:y'),
'ro', label='solution')
axes[0].plot(sim_out.get_val('traj.phase0.timeseries.states:x'),
sim_out.get_val('traj.phase0.timeseries.states:y'),
'b-', label='simulation')
axes[0].set_xlabel('x (m)')
axes[0].set_ylabel('y (m/s)')
axes[0].legend()
axes[0].grid()
axes[1].plot(p.get_val('traj.phase0.timeseries.time'),
p.get_val('traj.phase0.timeseries.controls:theta', units='deg'),
'ro', label='solution')
axes[1].plot(sim_out.get_val('traj.phase0.timeseries.time'),
sim_out.get_val('traj.phase0.timeseries.controls:theta', units='deg'),
'b-', label='simulation')
axes[1].set_xlabel('time (s)')
axes[1].set_ylabel(r'$\theta$ (deg)')
axes[1].legend()
axes[1].grid()
plt.show()
--- Constraint Report [traj] ---
--- phase0 ---
None
INFO: checking out_of_order
INFO:check_config:checking out_of_order
INFO: checking system
INFO:check_config:checking system
INFO: checking solvers
INFO:check_config:checking solvers
INFO: checking dup_inputs
INFO:check_config:checking dup_inputs
INFO: checking missing_recorders
INFO:check_config:checking missing_recorders
WARNING: The Problem has no recorder of any kind attached
WARNING:check_config:The Problem has no recorder of any kind attached
INFO: checking unserializable_options
INFO:check_config:checking unserializable_options
INFO: checking comp_has_no_outputs
INFO:check_config:checking comp_has_no_outputs
INFO: checking auto_ivc_warnings
INFO:check_config:checking auto_ivc_warnings
Full total jacobian was computed 3 times, taking 0.090990 seconds.
Total jacobian shape: (31, 50)
Jacobian shape: (31, 50) (13.81% nonzero)
FWD solves: 1 REV solves: 6
Total colors vs. total size: 7 vs 31 (77.4% improvement)
Sparsity computed using tolerance: 1e-25
Time to compute sparsity: 0.090990 sec.
Time to compute coloring: 0.029415 sec.
Memory to compute coloring: 0.542969 MB.
Optimization terminated successfully (Exit mode 0)
Current function value: [1.80160471]
Iterations: 46
Function evaluations: 55
Gradient evaluations: 46
Optimization Complete
-----------------------------------
[1.80160471]
Simulating trajectory traj
Done simulating trajectory traj